Inhalt

• Kurze Zusammenfassung
• Schritte
• Teil 1 von 3: Testen der Teilbarkeit von Matrizen
• Teil 2 von 3: Finden der inversen Matrix
• Teil 3 von 3: Matrixmultiplikation
• Tipps
• Warnungen
• Zusätzliche Artikel

Wenn Sie wissen, wie man zwei Matrizen multipliziert, können Sie mit dem „Teilen“ der Matrizen beginnen. Das Wort „Division“ steht in Anführungszeichen, da Matrizen eigentlich nicht geteilt werden können. Die Divisionsoperation wird durch die Operation des Multiplizierens einer Matrix mit einer Matrix ersetzt, die die Umkehrung der zweiten Matrix ist. Betrachten Sie der Einfachheit halber ein Beispiel mit ganzen Zahlen: 10 ÷ 5. Finden Sie den Kehrwert von 5: 5 oder /₅, und dann Division durch Multiplikation ersetzen: 10 x 5; das Ergebnis von Division und Multiplikation ist das gleiche. Daher wird angenommen, dass die Division durch die Multiplikation mit der inversen Matrix ersetzt werden kann. Typischerweise werden solche Berechnungen verwendet, um lineare Gleichungssysteme zu lösen.

Kurze Zusammenfassung

1. Matrizen können nicht geteilt werden. Anstatt zu dividieren, wird eine Matrix mit der Umkehrung der zweiten Matrix multipliziert. "Division" von zwei Matrizen [A] ÷ [B] wird wie folgt geschrieben: [A] * [B] oder [B] * [A].
2. Wenn die Matrix [B] nicht quadratisch ist oder ihre Determinante 0 ist, schreiben Sie "keine eindeutige Lösung". Finden Sie andernfalls die Determinante der Matrix [B] und fahren Sie mit dem nächsten Schritt fort.
3. Finden Sie das Gegenteil: [B].
4. Multiplizieren Sie die Matrizen, um [A] * [B] oder [B] * [A] zu finden. Beachten Sie, dass die Reihenfolge, in der die Matrizen multipliziert werden, das Endergebnis beeinflusst (dh die Ergebnisse können variieren).

Schritte

Teil 1 von 3: Testen der Teilbarkeit von Matrizen

1. 1 Verstehen Sie die "Aufteilung" von Matrizen. Tatsächlich können Matrizen nicht geteilt werden. Es gibt keine mathematische Operation wie das „Teilen einer Matrix durch eine andere“. Die Division wird durch Multiplizieren einer Matrix mit dem Inversen der zweiten Matrix ersetzt. Das heißt, die Notation [A] ÷ [B] ist nicht korrekt und wird durch die folgende Notation ersetzt: [A] * [B]. Da bei skalaren Werten beide Einträge äquivalent sind, können wir theoretisch von einer "Aufteilung" von Matrizen sprechen, aber es ist immer noch besser, die richtige Terminologie zu verwenden.
   • Beachten Sie, dass [A] * [B] und [B] * [A] unterschiedliche Operationen sind. Es kann notwendig sein, beide Operationen durchzuführen, um alle möglichen Lösungen zu finden.
   • Zum Beispiel statt ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} div { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ aufschreiben ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} }$.
     Möglicherweise müssen Sie berechnen ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} * { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} }$um ein anderes Ergebnis zu erhalten.
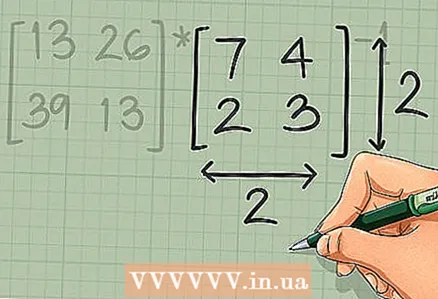2. 2 Stellen Sie sicher, dass die Matrix, durch die Sie die andere Matrix „teilen“, quadratisch ist. Um eine Matrix zu invertieren (die Inverse einer Matrix zu finden), muss sie quadratisch sein, d. h. mit der gleichen Anzahl von Zeilen und Spalten. Wenn die invertierte Matrix nicht invers ist, gibt es keine eindeutige Lösung.
   • Auch hier sind die Matrizen nicht "teilbar". In der Operation [A] * [B] bezieht sich die beschriebene Bedingung auf die Matrix [B]. In unserem Beispiel bezieht sich diese Bedingung auf die Matrix ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$
   • Eine Matrix, die invertiert werden kann, heißt nicht entartet oder regulär. Eine Matrix, die nicht invertiert werden kann, heißt entartet oder singulär.
3. 3 Prüfen Sie, ob die beiden Matrizen multipliziert werden können. Um zwei Matrizen zu multiplizieren, muss die Anzahl der Spalten in der ersten Matrix gleich der Anzahl der Zeilen in der zweiten Matrix sein. Ist diese Bedingung im Eintrag [A] * [B] oder [B] * [A] nicht erfüllt, gibt es keine Lösung.
   • Wenn beispielsweise die Größe der Matrix [A] 4 x 3 beträgt und die Größe der Matrix [B] 2 x 2 beträgt, gibt es keine Lösung. Sie können [A] * [B] nicht multiplizieren, weil 4 2, und Sie können [B] * [A] nicht multiplizieren, weil 2 ≠ 3.
   • Beachten Sie, dass die inverse Matrix [B] immer die gleiche Anzahl von Zeilen und Spalten hat wie die ursprüngliche Matrix [B]. Es ist nicht notwendig, die inverse Matrix zu finden, um zu überprüfen, ob zwei Matrizen multipliziert werden können.
   • In unserem Beispiel beträgt die Größe beider Matrizen 2 x 2, sodass sie in beliebiger Reihenfolge multipliziert werden können.
4. 4 Finden Sie die Determinante der 2 × 2-Matrix. Denken Sie daran: Sie können eine Matrix nur invertieren, wenn ihre Determinante nicht Null ist (andernfalls können Sie die Matrix nicht invertieren). So finden Sie die Determinante einer 2 x 2 Matrix:
   • 2 x 2-Matrix: Determinante einer Matrix ${ displaystyle { begin {pmatrix} a & b c & d end {pmatrix}}}$ ist gleich ad - bc. Das heißt, vom Produkt der Elemente der Hauptdiagonale (durchläuft die obere linke und untere rechte Ecke) die Produkte der Elemente der anderen Diagonale (durchläuft die obere rechte und untere linke Ecke) subtrahieren.
   • Zum Beispiel die Determinante der Matrix ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ gleich (7) (3) - (4) (2) = 21 - 8 = 13. Die Determinante ist ungleich null, daher kann diese Matrix invertiert werden.
5. 5 Finden Sie die Determinante der größeren Matrix. Wenn die Größe der Matrix 3 x 3 oder mehr beträgt, ist die Determinante etwas schwieriger zu berechnen.
   • 3 x 3 Matrix: Wählen Sie ein beliebiges Element aus und streichen Sie die Zeile und Spalte durch, in der es sich befindet.Finden Sie die Determinante der resultierenden 2 × 2-Matrix und multiplizieren Sie sie dann mit dem ausgewählten Element; Geben Sie das Vorzeichen der Determinante in einer speziellen Tabelle an. Wiederholen Sie diesen Vorgang für die anderen beiden Elemente, die sich in derselben Zeile oder Spalte wie das ausgewählte Element befinden. Berechnen Sie dann die Summe der (drei) erhaltenen Determinanten. Lesen Sie diesen Artikel, um weitere Informationen zum Bestimmen der Determinante einer 3 x 3 Matrix zu erhalten.
   • Große Matrizen: Die Determinante solcher Matrizen wird am besten mit einem Grafikrechner oder einer Software gesucht. Die Methode ähnelt der Methode zum Auffinden der Determinante einer 3 × 3-Matrix, ist jedoch ziemlich mühsam, sie manuell anzuwenden. Um beispielsweise die Determinante einer 4 x 4-Matrix zu finden, müssen Sie die Determinanten von vier 3 x 3-Matrizen finden.
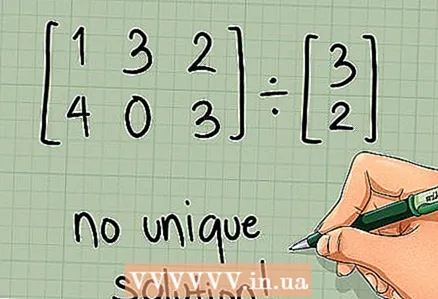6. 6 Berechnungen fortsetzen. Wenn die Matrix nicht quadratisch ist oder ihre Determinante gleich Null ist, schreiben Sie "keine eindeutige Lösung", dh der Berechnungsprozess ist abgeschlossen. Wenn die Matrix quadratisch ist und eine Determinante ungleich null hat, fahren Sie mit dem nächsten Abschnitt fort.

Teil 2 von 3: Finden der inversen Matrix

1. 1 Vertausche die Elemente der Hauptdiagonalen der 2 x 2 Matrix. Verwenden Sie bei einer 2 × 2-Matrix die schnelle inverse Methode. Vertauschen Sie zuerst das obere linke Element und das untere rechte Element. Beispielsweise:
   • ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & 4 2 & 7 end {pmatrix}}}$
   • Notiz: Die meisten Leute verwenden Taschenrechner, um eine 3 x 3 (oder größere) Matrix zu invertieren. Wenn Sie dies manuell tun müssen, gehen Sie zum Ende dieses Abschnitts.
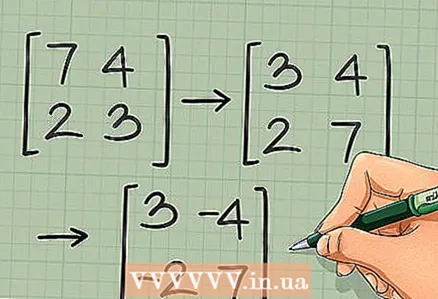2. 2 Vertauschen Sie die verbleibenden beiden Elemente nicht, sondern ändern Sie ihr Vorzeichen. Das heißt, multiplizieren Sie das obere rechte Element und das untere linke Element mit -1:
   • ${ displaystyle { begin {pmatrix} 3 & 4 2 & 7 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
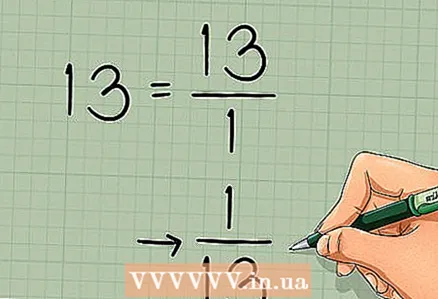3. 3 Finden Sie den Kehrwert der Determinante. Die Determinante dieser Matrix wurde im vorherigen Abschnitt gefunden, daher werden wir sie nicht erneut berechnen. Die Umkehrung der Determinante wird wie folgt geschrieben: 1 / (Determinante):
   • In unserem Beispiel ist die Determinante 13. Kehrwert: ${ displaystyle { frac {1} {13}}}$.
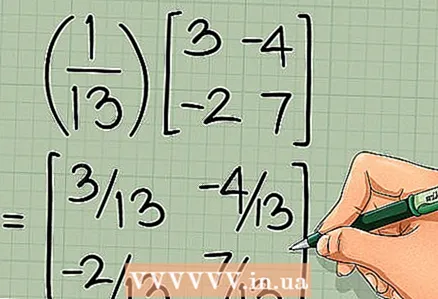4. 4 Multiplizieren Sie die resultierende Matrix mit dem Kehrwert der Determinante. Multiplizieren Sie jedes Element der neuen Matrix mit dem Inversen der Determinante. Die endgültige Matrix ist die Umkehrung der ursprünglichen 2 x 2-Matrix:
   • ${ displaystyle { frac {1} {13}} * { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
     =${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}}}$
5. 5 Überprüfen Sie, ob die Berechnungen korrekt sind. Multiplizieren Sie dazu die ursprüngliche Matrix mit ihrer Umkehrung. Wenn die Berechnungen korrekt sind, ergibt das Produkt der ursprünglichen Matrix durch die Inverse die Identitätsmatrix: ${ displaystyle { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}$... Wenn der Test erfolgreich war, fahren Sie mit dem nächsten Abschnitt fort.
   • In unserem Beispiel: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} = { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}$.
   • Weitere Informationen zum Multiplizieren von Matrizen finden Sie in diesem Artikel.
   • Hinweis: Die Operation der Matrixmultiplikation ist nicht kommutativ, dh die Reihenfolge der Matrizen ist wichtig. Aber wenn die ursprüngliche Matrix mit ihrer Umkehrung multipliziert wird, führt jede Reihenfolge zur Identitätsmatrix.
6. 6 Finden Sie die Inverse einer 3 x 3 Matrix (oder größer). Wenn Sie mit diesem Verfahren bereits vertraut sind, verwenden Sie besser einen Grafikrechner oder eine spezielle Software. Wenn Sie die inverse Matrix manuell finden müssen, wird der Vorgang im Folgenden kurz beschrieben:
   • Verbinden Sie die Identitätsmatrix I auf der rechten Seite der ursprünglichen Matrix. Zum Beispiel [B] → [B | ICH]. Für die Identitätsmatrix sind alle Elemente der Hauptdiagonalen gleich 1 und alle anderen Elemente sind gleich 0.
   • Vereinfachen Sie die Matrix so, dass ihre linke Seite gestuft wird; Vereinfachen Sie weiter, sodass die linke Seite die Identitätsmatrix wird.
   • Nach Vereinfachung hat die Matrix folgende Form: [I | B]. Das heißt, seine rechte Seite ist die Umkehrung der ursprünglichen Matrix.

Teil 3 von 3: Matrixmultiplikation

1. 1 Schreiben Sie zwei mögliche Ausdrücke auf. Die Multiplikation zweier Skalare ist kommutativ, dh 2 x 6 = 6 x 2.Dies ist bei der Matrixmultiplikation nicht der Fall, daher müssen Sie möglicherweise zwei Ausdrücke lösen:
   • x = [A] * [B] ist die Lösung der Gleichung x[B] = [A].
   • x = [B] * [A] ist die Lösung von Gleichung [B]x = [A].
   • Führen Sie jede mathematische Operation auf beiden Seiten der Gleichung durch. Wenn [A] = [C] dann [B] [A] ≠ [C] [B] weil [B] links von [A] aber rechts von [C] ist.
2. 2 Bestimmen Sie die Größe der endgültigen Matrix. Die Größe der endgültigen Matrix hängt von der Größe der multiplizierten Matrizen ab. Die Anzahl der Zeilen in der Endmatrix entspricht der Anzahl der Zeilen in der ersten Matrix und die Anzahl der Spalten in der Endmatrix entspricht der Anzahl der Spalten in der zweiten Matrix.
   • In unserem Beispiel ist die Größe beider Matrizen ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}}}$ und ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}}}$ ist 2 x 2, so dass die Größe der ursprünglichen Matrix 2 x 2 beträgt.
   • Betrachten Sie ein komplexeres Beispiel: Wenn die Größe der Matrix [A] 4 x 3, und die Größe der Matrix [B] beträgt 3 x 3, dann ist die endgültige Matrix [A] * [B] 4 x 3.
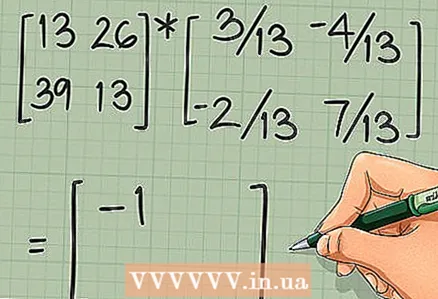3. 3 Finden Sie den Wert des ersten Elements. Lesen Sie diesen Artikel oder erinnern Sie sich an die folgenden grundlegenden Schritte:
   • Um das erste Element (erste Zeile, erste Spalte) der endgültigen Matrix [A] [B] zu finden, berechnen Sie das Skalarprodukt der Elemente der ersten Zeile der Matrix [A] und der Elemente der ersten Spalte der Matrix [B ]. Bei einer 2 x 2 Matrix berechnet sich das Skalarprodukt wie folgt: ${ displaystyle a_ {1,1} * b_ {1,1} + a_ {1,2} * b_ {2,1}}$.
   • In unserem Beispiel: ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} & { frac {-4} { 13}} { frac {-2} {13}} & { frac {7} {13}} end {pmatrix}}}$... Somit ist das erste Element der endgültigen Matrix das Element:
     ${ Displaystil (13 * { frac {3} {13}}) + (26 * { frac {-2} {13}})}$
     ${ Anzeigestil = 3 + -4}$
     ${ Anzeigestil = -1}$
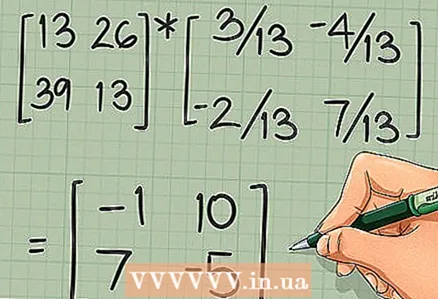4. 4 Fahren Sie mit der Berechnung der Punktprodukte fort, um jedes Element der endgültigen Matrix zu finden. Beispielsweise ist das in der zweiten Reihe und der ersten Spalte befindliche Element gleich dem Skalarprodukt der zweiten Reihe der Matrix [A] und der ersten Spalte der Matrix [B]. Versuchen Sie, die restlichen Elemente selbst zu finden. Sie sollten folgende Ergebnisse erhalten:
   • ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} & { frac {-4} { 13}} { frac {-2} {13}} & { frac {7} {13}} end {pmatrix}} = { begin {pmatrix} -1 & 10 7 & -5 end {pmatrix}}}$
   • Wenn Sie eine andere Lösung finden müssen: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} = { begin {pmatrix} -9 & 2 19 & 3 Ende {pmatrix}}}$

Tipps

• Die Matrix kann in einen Skalar unterteilt werden; dazu wird jedes Element der Matrix durch einen Skalar geteilt.
  • Wenn zum Beispiel die Matrix ${ displaystyle { begin {pmatrix} 6 & 8 2 & 4 end {pmatrix}}}$ geteilt durch 2 erhält man die Matrix ${ displaystyle { begin {pmatrix} 3 & 4 1 & 2 end {pmatrix}}}$

Warnungen

• Bei Matrixberechnungen liefert der Rechner nicht immer absolut genaue Ergebnisse. Wenn der Rechner beispielsweise behauptet, dass das Element eine sehr kleine Zahl ist (z. B. 2E), ist der Wert höchstwahrscheinlich null.

Zusätzliche Artikel

Wie man Matrizen multipliziert So finden Sie die Inverse einer 3x3-Matrix So finden Sie die Determinante einer 3X3-Matrix So finden Sie das Maximum oder Minimum einer quadratischen Funktion So berechnen Sie die Frequenz Wie man quadratische Gleichungen löst So messen Sie die Höhe ohne Maßband So finden Sie die Quadratwurzel einer Zahl manuell Milliliter in Gramm umrechnen So konvertieren Sie von binär in dezimal So berechnen Sie den Pi-Wert So konvertieren Sie von dezimal in binär Wie berechnet man die Wahrscheinlichkeit So konvertieren Sie Minuten in Stunden