Inhalt

• Schritte
• Teil 1 von 3: Transponiere die Matrix
• Teil 2 von 3: Transpositionseigenschaften
• Teil 3 von 3: Hermitesche konjugierte Matrix mit komplexen Elementen
• Tipps

Wenn Sie lernen, Matrizen zu transponieren, werden Sie ihre Struktur besser verstehen. Sie kennen vielleicht bereits quadratische Matrizen und ihre Symmetrie, um die Transposition zu meistern. Unter anderem hilft die Transposition dabei, Vektoren in Matrixform umzuwandeln und Vektorprodukte zu finden. Bei der Arbeit mit komplexen Matrizen können hermitesch-konjugierte (konjugiert-transponierte) Matrizen Ihnen bei der Lösung einer Vielzahl von Problemen helfen.

Schritte

Teil 1 von 3: Transponiere die Matrix

1. 1 Nehmen Sie eine beliebige Matrix. Jede Matrix kann unabhängig von der Anzahl der Zeilen und Spalten transponiert werden. In den meisten Fällen müssen quadratische Matrizen mit der gleichen Anzahl von Zeilen und Spalten transponiert werden. Betrachten Sie daher der Einfachheit halber die folgende Matrix als Beispiel:
   • die Matrix EIN =
     1  2  3
     4  5  6
     7  8  9
2. 2 Stellen Sie sich die erste Zeile einer direkten Matrix als erste Spalte der transponierten Matrix vor. Schreiben Sie einfach die erste Zeile als Spalte:
   • transponierte Matrix = A
   • erste Spalte von Matrix A:
     1
     2
     3
3. 3 Machen Sie dasselbe für den Rest der Zeilen. Die zweite Zeile der Originalmatrix wird zur zweiten Spalte der transponierten Matrix. Alle Zeilen in Spalten übersetzen:
   • EIN =
     1  4  7
     2  5  8
     3  6  9
4. 4 Versuchen Sie, eine nicht quadratische Matrix zu transponieren. Jede rechteckige Matrix kann auf die gleiche Weise transponiert werden. Schreiben Sie einfach die erste Zeile als erste Spalte, die zweite Zeile als zweite Spalte und so weiter. Im folgenden Beispiel ist jede Zeile der Originalmatrix mit einer eigenen Farbe markiert, um deutlicher zu machen, wie sie beim Transponieren transformiert wird:
   • die Matrix Z =
     4  7  2  1
     3  9  8  6
   • die Matrix Z =
     4  3
     7  9
     2  8
     1  6
5. 5 Lassen Sie uns die Transposition in Form einer mathematischen Notation ausdrücken. Obwohl die Idee der Umsetzung sehr einfach ist, ist es am besten, sie als strenge Formel aufzuschreiben. Die Matrixnotation erfordert keine besonderen Begriffe:
   • Angenommen eine gegebene Matrix B bestehend aus m x n Elemente (m Zeilen und n Spalten), dann ist die transponierte Matrix B eine Menge von n x m Elemente (n Zeilen und m Spalten).
   • Für jedes Element b_xy (Linie x und Spalte ja) der Matrix B in der Matrix B existiert ein äquivalentes Element b_yx (Linie ja und Spalte x).

Teil 2 von 3: Transpositionseigenschaften

1. 1 (M = M. Nach doppelter Transposition erhält man die Originalmatrix. Dies ist ziemlich offensichtlich, da Sie beim erneuten Transponieren die Zeilen und Spalten erneut ändern, was zur ursprünglichen Matrix führt.
2. 2 Spiegeln Sie die Matrix um die Hauptdiagonale. Quadratische Matrizen können relativ zur Hauptdiagonalen "gespiegelt" werden. Außerdem sind die Elemente entlang der Hauptdiagonalen (von a₁₁ in die rechte untere Ecke der Matrix) bleiben an Ort und Stelle, und die restlichen Elemente bewegen sich auf die andere Seite dieser Diagonale und bleiben im gleichen Abstand davon.
   • Wenn Sie sich diese Methode nur schwer vorstellen können, nehmen Sie ein Blatt Papier und zeichnen Sie eine 4x4-Matrix. Dann ordnen Sie seine Seitenelemente relativ zur Hauptdiagonalen neu an. Verfolgen Sie gleichzeitig die Elemente a₁₄ und ein₄₁... Beim Transponieren müssen sie wie andere Paare von Seitenelementen vertauscht werden.
3. 3 Transponiere die symmetrische Matrix. Die Elemente einer solchen Matrix sind um die Hauptdiagonale symmetrisch. Wenn Sie die obige Operation ausführen und die symmetrische Matrix "spiegeln", ändert sie sich nicht. Alle Elemente ändern sich in ähnliche. Tatsächlich ist dies die Standardmethode, um zu bestimmen, ob eine bestimmte Matrix symmetrisch ist. Wenn die Gleichheit A = A gilt, dann ist die Matrix A symmetrisch.

Teil 3 von 3: Hermitesche konjugierte Matrix mit komplexen Elementen

1. 1 Betrachten Sie eine komplexe Matrix. Die Elemente einer komplexen Matrix bestehen aus Real- und Imaginärteilen. Eine solche Matrix kann auch transponiert werden, obwohl in den meisten praktischen Anwendungen konjugiert-transponierte oder hermitesch-konjugierte Matrizen verwendet werden.
   • Gegeben sei eine Matrix C =
     2+ich     3-2ich
     0+ich     5+0ich
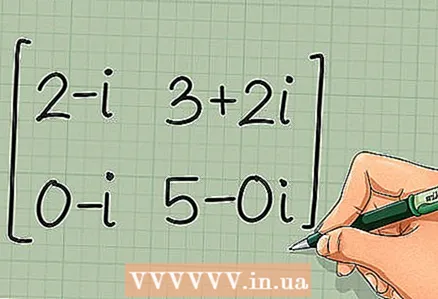2. 2 Ersetze die Elemente durch komplex konjugierte Zahlen. Bei der komplexen Konjugation bleibt der Realteil gleich und der Imaginärteil ändert sein Vorzeichen ins Gegenteil. Machen wir dies mit allen vier Elementen der Matrix.
   • finde die komplex konjugierte Matrix C * =
     2-ich     3+2ich
     0-ich     5-0ich
3. 3 Wir transponieren die resultierende Matrix. Nehmen Sie die gefundene komplex konjugierte Matrix und transponieren Sie sie einfach. Als Ergebnis erhalten wir eine konjugiert-transponierte (hermitesch-konjugierte) Matrix.
   • die konjugiert-transponierte Matrix C =
     2-ich        0-ich
     3+2ich     5-0ich

Tipps

• In diesem Artikel wird die gegenüber der Matrix A transponierte Matrix mit A bezeichnet. Es gibt auch die Notation A' oder Ã.
• In diesem Artikel wird die hermitesch-konjugierte Matrix in Bezug auf die Matrix A als A bezeichnet, was eine gängige Notation in der linearen Algebra ist. In der Quantenmechanik wird häufig die Notation A verwendet.Manchmal wird eine hermitesche konjugierte Matrix in der Form A * geschrieben, aber es ist besser, diese Notation zu vermeiden, da sie auch zum Schreiben einer komplex konjugierten Matrix verwendet wird.