Inhalt

• Schritte
• Tipps

Die rationale Funktion hat die Form y = N (x) / D (x), wobei N und D Polynome sind. Um eine solche Funktion genau darzustellen, benötigen Sie gute Kenntnisse der Algebra, einschließlich Differentialrechnungen. Betrachten Sie das folgende Beispiel: ja = (2x - 6x + 5)/(4x + 2).

Schritte

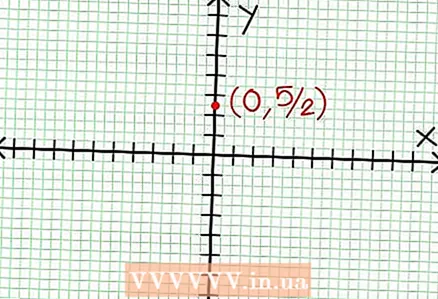1. 1 Finden Sie den y-Achsenabschnitt des Graphen. Setzen Sie dazu x = 0 in die Funktion ein und erhalten Sie y = 5/2. Somit hat der Schnittpunkt des Graphen mit der Y-Achse Koordinaten (0, 5/2).Platzieren Sie diesen Punkt auf der Koordinatenebene.
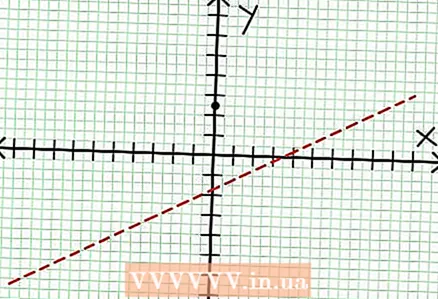2. 2 Finden Sie die horizontalen Asymptoten. Teilen Sie den Zähler durch den Nenner (in einer Spalte), um das Verhalten von "y" mit Werten von "x" gegen unendlich zu bestimmen. In unserem Beispiel lautet die Aufteilung ja = (1/2)x - (7/4) + 17/(8x +4). Für große positive oder negative Werte von "x" 17 / (8x + 4) geht gegen Null und der Graph nähert sich der durch die Funktion gegebenen Geraden ja = (1/2)x - (7/4). Zeichnen Sie diese Funktion mithilfe der gestrichelten Linie.
   • Ist der Zählergrad kleiner als der Nennergrad, dann kann man den Zähler nicht durch den Nenner dividieren und die Asymptote wird durch die Funktion . beschrieben bei = 0.
   • Wenn der Grad des Zählers gleich dem Grad des Nenners ist, dann ist die Asymptote eine horizontale Linie gleich dem Verhältnis der Koeffizienten bei "x" im höchsten Grad.
   • Wenn der Grad des Zählers 1 größer ist als der Grad des Nenners, dann ist die Asymptote eine geneigte Gerade, deren Steigung gleich dem Verhältnis der Koeffizienten bei "x" zum höchsten Grad ist.
   • Wenn der Grad des Zählers um 2, 3 usw. größer ist als der Grad des Nenners, dann für große Werte |NS| Bedeutung bei gegen unendlich (positiv oder negativ) in Form eines quadratischen, kubischen oder anderen Grades eines Polynoms neigen. In diesem Fall müssen Sie höchstwahrscheinlich keinen exakten Graphen der Funktion erstellen, die Sie erhalten, indem Sie den Zähler durch den Nenner dividieren.
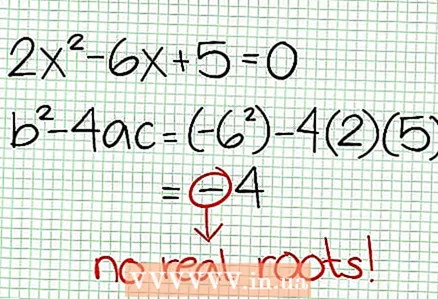3. 3 Finden Sie die Nullstellen der Funktion. Eine rationale Funktion hat Nullen, wenn ihr Zähler null ist, also N (NS) = 0. In unserem Beispiel 2x - 6x + 5 = 0. Die Diskriminante dieser quadratischen Gleichung: B - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Da die Diskriminante negativ ist, ist N (NS), und damit F (NS) hat keine wirklichen Wurzeln. Der Graph einer rationalen Funktion schneidet die X-Achse nicht.Wenn die Funktion Nullstellen (Wurzeln) hat, dann lege sie auf die Koordinatenebene.
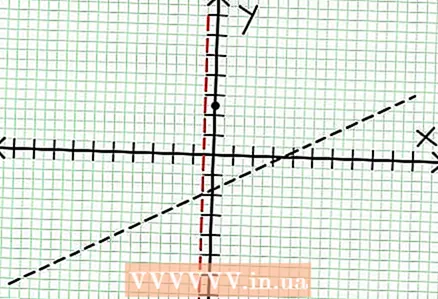4. 4 Finden Sie die vertikalen Asymptoten. Setzen Sie dazu den Nenner auf Null. In unserem Beispiel 4x + 2 = 0 und NS = -1/2. Zeichnen Sie die vertikale Asymptote mit der gestrichelten Linie. Wenn für einen gewissen Wert NS N (NS) = 0 und D (NS) = 0, dann existiert die vertikale Asymptote entweder oder existiert nicht (dies ist ein seltener Fall, aber es ist besser, sich daran zu erinnern).
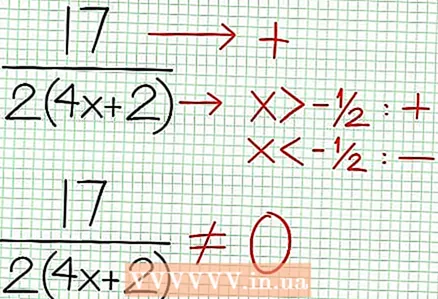5. 5 Betrachten Sie den Rest des Zählers geteilt durch den Nenner. Ist es positiv, negativ oder null? In unserem Beispiel ist der Rest 17, was positiv ist. Nenner 4x + 2 positiv rechts von der vertikalen Asymptote und negativ links davon. Dies bedeutet, dass der Graph der rationalen Funktion für große positive Werte NS nähert sich der Asymptote von oben und für große negative Werte NS - von unten. Seit 17 / (8x + 4) nie gleich Null ist, dann schneidet der Graph dieser Funktion niemals die durch die Funktion angegebene Gerade bei = (1/2)NS - (7/4).
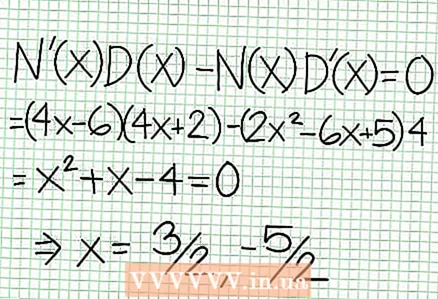6. 6 Lokale Extrema finden. Ein lokales Extremum existiert für N '(x) D (x) - N (x) D '(x) = 0. In unserem Beispiel ist N ’(x) = 4x - 6 und D '(x) = 4. N ’(x) D (x) - N (x) D '(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Wenn Sie diese Gleichung lösen, finden Sie, dass x = 3/2 und x = -5/2. (Dies sind nicht ganz genaue Werte, aber sie sind für unseren Fall geeignet, wenn keine Superpräzision erforderlich ist.)
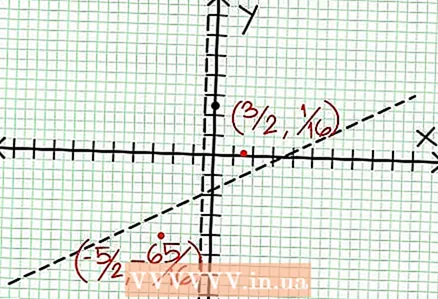7. 7 Finde den Wert bei für jedes lokale Extremum. Ersetzen Sie dazu die Werte NS in die ursprüngliche rationale Funktion. In unserem Beispiel ist f (3/2) = 1/16 und f (-5/2) = -65/16. Legen Sie die Punkte (3/2, 1/16) und (-5/2, -65/16) auf der Koordinatenebene beiseite. Da die Berechnungen auf ungefähren Werten (aus dem vorherigen Schritt) basieren, sind das gefundene Minimum und Maximum auch nicht ganz genau (aber wahrscheinlich sehr nahe an den genauen Werten). (Der Punkt (3/2, 1/16) liegt sehr nahe am lokalen Minimum. Ab Schritt 3 wissen wir, dass bei immer positiv für NS> -1/2, und wir fanden einen kleinen Wert (1/16); daher ist der Fehlerwert in diesem Fall extrem klein.)
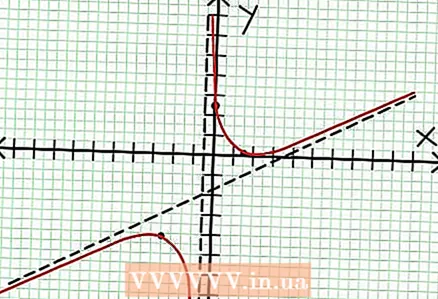8. 8 Verbinden Sie die ausstehenden Punkte und verlängern Sie den Graphen sanft zu den Asymptoten (vergessen Sie nicht die richtige Richtung des Graphen, der sich den Asymptoten nähert). Denken Sie daran, dass der Graph die X-Achse nicht kreuzen darf (siehe Schritt 3). Der Graph schneidet sich auch nicht mit den horizontalen und vertikalen Asymptoten (siehe Schritt 5). Ändern Sie die Richtung des Diagramms nur an den im vorherigen Schritt gefundenen Extrempunkten.

Tipps

• Wenn Sie die obigen Schritte strikt der Reihe nach befolgt haben, müssen Sie die zweite Ableitung (oder ähnliche komplexe Größen) nicht berechnen, um Ihre Lösung zu testen.
• Wenn Sie die Werte von Größen nicht berechnen müssen, können Sie das Finden lokaler Extrema durch die Berechnung einiger zusätzlicher Koordinatenpaare ersetzen (NS, bei) zwischen jedem Asymptotenpaar. Wenn es Ihnen egal ist, wie die beschriebene Methode funktioniert, wundern Sie sich nicht, warum Sie die Ableitung nicht finden und die Gleichung N lösen können '(x) D (x) - N (x) D '(x) = 0.
• In einigen Fällen müssen Sie mit Polynomen höherer Ordnung arbeiten. Wenn Sie die genaue Lösung nicht durch Faktorisierung, Formeln usw. finden können, schätzen Sie mögliche Lösungen mit numerischen Methoden wie der Newton-Methode.
• In seltenen Fällen haben Zähler und Nenner einen gemeinsamen variablen Faktor. Dies führt gemäß den beschriebenen Schritten zu einer Null und einer vertikalen Asymptote an derselben Stelle. Dies ist jedoch nicht möglich, und die Erklärung ist eine der folgenden:
  • Null in N (NS) hat eine höhere Multiplizität als Null in D (NS). Grafik F (NS) geht an dieser Stelle gegen Null, ist dort aber nicht definiert. Zeigen Sie dies an, indem Sie einen Kreis um den Punkt ziehen.
  • Null in N (NS) und Null in D (NS) haben die gleiche Multiplizität. Der Graph nähert sich bei diesem Wert einem Punkt ungleich Null NSaber darin nicht definiert. Zeigen Sie dies an, indem Sie einen Kreis um den Punkt ziehen.
  • Null in N (NS) hat eine kleinere Multiplizität als Null in D (NS). Hier liegt eine vertikale Asymptote vor.