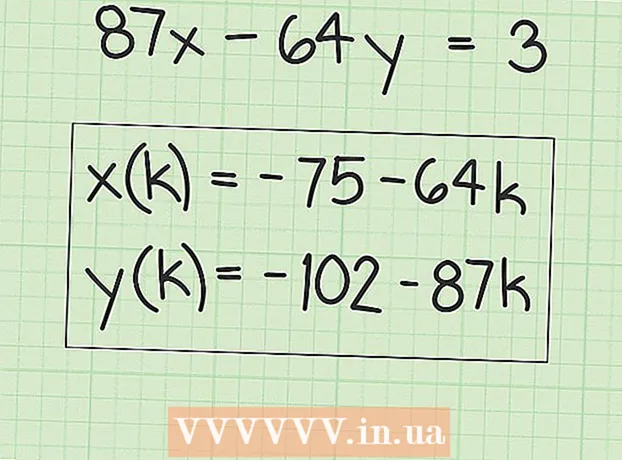
Inhalt

• Schritte
• Teil 1 von 4: Wie man eine Gleichung schreibt
• Teil 2 von 4: So schreiben Sie den Euklid-Algorithmus
• Teil 3 von 4: So finden Sie eine Lösung mit dem Algorithmus von Euklid
• Teil 4 von 4: Unendlich andere Lösungen finden

Um eine lineare diophantische Gleichung zu lösen, müssen Sie die Werte der Variablen "x" und "y" finden, bei denen es sich um ganze Zahlen handelt. Eine ganzzahlige Lösung ist komplexer als üblich und erfordert einen bestimmten Satz von Aktionen. Zuerst müssen Sie den größten gemeinsamen Teiler (GCD) der Koeffizienten berechnen und dann eine Lösung finden. Sobald Sie eine ganzzahlige Lösung für eine lineare Gleichung gefunden haben, können Sie ein einfaches Muster verwenden, um unendlich viele andere Lösungen zu finden.

Schritte

Teil 1 von 4: Wie man eine Gleichung schreibt

1. 1 Schreiben Sie die Gleichung in Standardform auf. Eine lineare Gleichung ist eine Gleichung, bei der die Exponenten der Variablen 1 nicht überschreiten. Um eine solche lineare Gleichung zu lösen, schreiben Sie sie zunächst in Standardform. Die Standardform einer linearen Gleichung sieht so aus: ${ displaystyle Ax + By = C}$, wo ${ Anzeigestil A, B}$ und ${ Anzeigestil C}$ - ganze Zahlen.
   • Wenn die Gleichung in einer anderen Form angegeben wird, bringen Sie sie mit einfachen algebraischen Operationen in die Standardform. Zum Beispiel gegeben die Gleichung ${ Anzeigestil 23x + 4y-7x = -3y + 15}$... Geben Sie ähnliche Begriffe an und schreiben Sie die Gleichung wie folgt: ${ Anzeigestil 16x + 7y = 15}$.
2. 2 Vereinfachen Sie die Gleichung (wenn möglich). Wenn Sie die Gleichung in Standardform schreiben, sehen Sie sich die Koeffizienten an ${ Anzeigestil A, B}$ und ${ Anzeigestil C}$... Wenn diese Quoten eine GCD haben, teilen Sie alle drei Quoten durch diese. Die Lösung einer solchen vereinfachten Gleichung ist auch die Lösung der ursprünglichen Gleichung.
   • Wenn beispielsweise alle drei Koeffizienten gerade sind, teilen Sie sie durch mindestens 2. Zum Beispiel:
     • ${ Anzeigestil 42x + 36y = 48}$ (alle Mitglieder sind durch 2 teilbar)
     • ${ Anzeigestil 21x + 18y = 24}$ (jetzt sind alle Mitglieder durch 3 teilbar)
     • ${ Anzeigestil 7x + 6y = 8}$ (diese Gleichung kann nicht mehr vereinfacht werden)
3. 3 Überprüfe, ob die Gleichung gelöst werden kann. In einigen Fällen können Sie sofort feststellen, dass die Gleichung keine Lösungen hat. Wenn der Koeffizient "C" nicht durch die GCD der Koeffizienten "A" und "B" teilbar ist, hat die Gleichung keine Lösungen.
   • Wenn beispielsweise beide Koeffizienten ${ Anzeigestil A}$ und ${ Anzeigestil B}$ gerade sind, dann ist der Koeffizient ${ Anzeigestil C}$ muss eben sein. Aber falls ${ Anzeigestil C}$ seltsam, dann gibt es keine Lösung.
     • Die gleichung ${ Anzeigestil 2x + 4y = 21}$ keine ganzzahligen Lösungen.
     • Die gleichung ${ Anzeigestil 5x + 10y = 17}$ Es gibt keine ganzzahligen Lösungen, da die linke Seite der Gleichung durch 5 teilbar ist und die rechte Seite nicht.

Teil 2 von 4: So schreiben Sie den Euklid-Algorithmus

1. 1 Verstehen Sie den Algorithmus von Euklid. Es ist eine Reihe wiederholter Divisionen, bei denen der vorherige Rest als nächster Teiler verwendet wird. Der letzte Teiler, der die Zahlen ganzzahlig teilt, ist der größte gemeinsame Teiler (GCD) der beiden Zahlen.
   • Lassen Sie uns zum Beispiel die GCD der Zahlen 272 und 36 mit dem Euklid-Algorithmus finden:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Dividiere die größere Zahl (272) durch die kleinere (36) und achte auf den Rest (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - dividiere den vorherigen Teiler (36) durch den vorherigen Rest (20). Beachten Sie den neuen Rückstand (16);
     • ${ Displaystil 20 = 1 * 16 + 4}$ - dividiere den vorherigen Teiler (20) durch den vorherigen Rest (16). Beachte den neuen Rückstand (4);
     • ${ Displaystil 16 = 4 * 4 + 0}$ - Dividiere den vorherigen Teiler (16) durch den vorherigen Rest (4). Da der Rest 0 ist, können wir sagen, dass 4 die GCD der ursprünglichen beiden Zahlen 272 und 36 ist.
2. 2 Wenden Sie den Euklid-Algorithmus auf die Koeffizienten "A" und "B" an. Wenn Sie die lineare Gleichung in Standardform schreiben, bestimmen Sie die Koeffizienten "A" und "B" und wenden Sie dann den Euklid-Algorithmus an, um die GCD zu finden. Zum Beispiel gegeben eine lineare Gleichung ${ Anzeigestil 87x-64y = 3}$.
   • Hier ist Euklids Algorithmus für die Koeffizienten A = 87 und B = 64:
     • ${ Anzeigestil 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ Anzeigestil 23 = 1 * 18 + 5}$
     • ${ Anzeigestil 18 = 3 * 5 + 3}$
     • ${ Anzeigestil 5 = 1 * 3 + 2}$
     • ${ Anzeigestil 3 = 1 * 2 + 1}$
     • ${ Anzeigestil 2 = 2 * 1 + 0}$
3. 3 Finden Sie den größten gemeinsamen Faktor (GCD). Da der letzte Teiler 1 war, sind GCD 87 und 64 1. Somit sind 87 und 64 Primzahlen relativ zueinander.
4. 4 Analysieren Sie das Ergebnis. Wenn Sie die gcd-Koeffizienten finden ${ Anzeigestil A}$ und ${ Anzeigestil B}$, vergleiche ihn mit dem Koeffizienten ${ Anzeigestil C}$ die ursprüngliche Gleichung. Ob ${ Anzeigestil C}$ teilbar durch gcd ${ Anzeigestil A}$ und ${ Anzeigestil B}$, die Gleichung hat eine ganzzahlige Lösung; andernfalls hat die Gleichung keine Lösungen.
   • Zum Beispiel die Gleichung ${ Anzeigestil 87x-64y = 3}$ kann gelöst werden, weil 3 durch 1 teilbar ist (gcd = 1).
   • Angenommen, GCD = 5. 3 ist nicht durch 5 teilbar, daher hat diese Gleichung keine ganzzahligen Lösungen.
   • Wenn eine Gleichung eine ganzzahlige Lösung hat, wie unten gezeigt, hat sie auch eine unendliche Anzahl anderer ganzzahliger Lösungen.

Teil 3 von 4: So finden Sie eine Lösung mit dem Algorithmus von Euklid

1. 1 Nummerieren Sie die Schritte zur Berechnung des GCD. Um die Lösung einer linearen Gleichung zu finden, müssen Sie den euklidischen Algorithmus als Grundlage für den Substitutions- und Vereinfachungsprozess verwenden.
   • Beginnen Sie mit der Nummerierung der Schritte zur Berechnung des GCD. Der Berechnungsprozess sieht wie folgt aus:
     • ${ displaystyle { text {Schritt 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Schritt 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Schritt 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Schritt 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Schritt 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Schritt 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Schritt 7}}: 2 = (2 * 1) +0}$
2. 2 Achten Sie auf den letzten Schritt, wo ein Rest verbleibt. Schreiben Sie die Gleichung für diesen Schritt um, um den Rest zu isolieren.
   • In unserem Beispiel ist der letzte Schritt mit Rest Schritt 6. Der Rest ist 1. Schreiben Sie die Gleichung in Schritt 6 wie folgt um:
     • ${ Anzeigestil 1 = 3- (1 * 2)}$
3. 3 Isolieren Sie den Rest des vorherigen Schritts. Dieser Prozess ist ein schrittweiser "Aufstieg". Jedes Mal werden Sie den Rest der Gleichung im vorherigen Schritt isolieren.
   • Isolieren Sie den Rest der Gleichung in Schritt 5:
     • ${ Anzeigestil 2 = 5- (1 * 3)}$ oder ${ Anzeigestil 2 = 5-3}$
4. 4 Ersetzen und vereinfachen. Beachten Sie, dass die Gleichung in Schritt 6 die Zahl 2 enthält und in der Gleichung in Schritt 5 die Zahl 2 isoliert ist. Anstelle von „2“ in der Gleichung in Schritt 6 ersetzen Sie den Ausdruck in Schritt 5:
   • ${ Anzeigestil 1 = 3-2}$ (Gleichung von Schritt 6)
   • ${ Anzeigestil 1 = 3- (5-3)}$ (statt 2 wurde ein Ausdruck ersetzt)
   • ${ Anzeigestil 1 = 3-5 + 3}$ (geöffnete Klammern)
   • ${ Anzeigestil 1 = 2 (3) -5}$ (vereinfacht)
5. 5 Wiederholen Sie den Substitutions- und Vereinfachungsprozess. Wiederholen Sie den beschriebenen Vorgang, indem Sie den euklidischen Algorithmus in umgekehrter Reihenfolge durchlaufen. Jedes Mal werden Sie die Gleichung aus dem vorherigen Schritt neu schreiben und in die letzte Gleichung einfügen, die Sie erhalten.
   • Der letzte Schritt, den wir uns angesehen haben, war Schritt 5. Gehen Sie also zu Schritt 4 und isolieren Sie den Rest in der Gleichung für diesen Schritt:
     • ${ Displaystil 3 = 18- (3 * 5)}$
   • Ersetzen Sie diesen Ausdruck für "3" in der letzten Gleichung:
     • ${ Anzeigestil 1 = 2 (18-3 * 5) -5}$
     • ${ Anzeigestil 1 = 2 (18) -6 (5) -5}$
     • ${ Anzeigestil 1 = 2 (18) -7 (5)}$
6. 6 Fahren Sie mit dem Ersetzungs- und Vereinfachungsprozess fort. Dieser Vorgang wird wiederholt, bis Sie den Anfangsschritt des euklidischen Algorithmus erreichen. Ziel des Prozesses ist es, die Gleichung mit den Koeffizienten 87 und 64 der zu lösenden Originalgleichung zu schreiben. In unserem Beispiel:
   • ${ Anzeigestil 1 = 2 (18) -7 (5)}$
   • ${ Anzeigestil 1 = 2 (18) -7 (23-18)}$ (ersetzt den Ausdruck aus Schritt 3)
     • ${ Anzeigestil 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ Anzeigestil 1 = 9 (18) -7 (23)}$
   • ${ Anzeigestil 1 = 9 (64-2 * 23) -7 (23)}$ (ersetzt den Ausdruck aus Schritt 2)
     • ${ Anzeigestil 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ Anzeigestil 1 = 9 (64) -25 (23)}$
   • ${ Anzeigestil 1 = 9 (64) -25 (87-64)}$ (ersetzt den Ausdruck aus Schritt 1)
     • ${ Anzeigestil 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ Anzeigestil 1 = 34 (64) -25 (87)}$
7. 7 Schreiben Sie die resultierende Gleichung gemäß den ursprünglichen Koeffizienten um. Wenn Sie zum ersten Schritt des euklidischen Algorithmus zurückkehren, werden Sie feststellen, dass die resultierende Gleichung zwei Koeffizienten der ursprünglichen Gleichung enthält. Schreiben Sie die Gleichung so um, dass die Reihenfolge ihrer Terme mit den Koeffizienten der ursprünglichen Gleichung übereinstimmt.
   • In unserem Beispiel ist die ursprüngliche Gleichung ${ Anzeigestil 87x-64y = 3}$... Schreiben Sie daher die resultierende Gleichung so um, dass die Koeffizienten in Einklang gebracht werden.Achten Sie besonders auf den Koeffizienten "64". In der ursprünglichen Gleichung ist dieser Koeffizient negativ und im euklidischen Algorithmus positiv. Daher muss der Faktor 34 negativ gemacht werden. Die endgültige Gleichung wird wie folgt geschrieben:
     • ${ Anzeigestil 87 (-25) -64 (-34) = 1}$
8. 8 Wenden Sie den entsprechenden Multiplikator an, um eine Lösung zu finden. Beachten Sie, dass in unserem Beispiel GCD = 1 ist, die endgültige Gleichung also 1 ist. Die ursprüngliche Gleichung (87x-64y) ist jedoch 3. Daher müssen alle Terme in der endgültigen Gleichung mit 3 multipliziert werden, um die Lösung zu erhalten:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ Anzeigestil 87 (-75) -64 (-102) = 3}$
9. 9 Schreiben Sie die ganzzahlige Lösung der Gleichung auf. Die Zahlen, die mit den Koeffizienten der ursprünglichen Gleichung multipliziert werden, sind die Lösungen dieser Gleichung.
   • Schreiben Sie in unserem Beispiel die Lösung als Koordinatenpaar: ${ Anzeigestil (x, y) = (- 75, -102)}$.

Teil 4 von 4: Unendlich andere Lösungen finden

1. 1 Verstehe, dass es unendlich viele Lösungen gibt. Wenn eine lineare Gleichung eine ganzzahlige Lösung hat, dann muss sie unendlich viele ganzzahlige Lösungen haben. Hier ist ein kurzer Beweis (in algebraischer Form):
   • ${ displaystyle Ax + By = C}$
   • ${ Anzeigestil A (x + B) + B (y-A) = C}$ (Wenn Sie "B" zu "x" addieren und "A" von "y" subtrahieren, ändert sich der Wert der ursprünglichen Gleichung nicht)
2. 2 Notieren Sie die ursprünglichen x- und y-Werte. Die Vorlage zur Berechnung der nächsten (unendlichen) Lösungen beginnt mit der einzigen Lösung, die Sie bereits gefunden haben.
   • In unserem Beispiel ist die Lösung ein Koordinatenpaar ${ Anzeigestil (x, y) = (- 75, -102)}$.
3. 3 Addieren Sie den "B"-Faktor zum "x"-Wert. Tun Sie dies, um den neuen x-Wert zu finden.
   • In unserem Beispiel ist x = -75 und B = -64:
     • ${ Anzeigestil x = -75 + (-64) = -139}$
   • Somit ist der neue Wert "x": x = -139.
4. 4 Subtrahieren Sie den Faktor "A" vom Wert "y". Damit sich der Wert der ursprünglichen Gleichung nicht ändert, müssen Sie beim Addieren einer Zahl zu "x" eine andere Zahl von "y" subtrahieren.
   • In unserem Beispiel ist y = -102 und A = 87:
     • ${ Anzeigestil y = -102-87 = -189}$
   • Somit ist der neue Wert für "y": y = -189.
   • Das neue Koordinatenpaar wird wie folgt geschrieben: ${ Anzeigestil (x, y) = (-139, -189)}$.
5. 5 Überprüfen Sie die Lösung. Um zu überprüfen, ob das neue Koordinatenpaar eine Lösung der ursprünglichen Gleichung ist, setzen Sie die Werte in die Gleichung ein.
   • ${ Anzeigestil 87x-64y = 3}$
   • ${ Anzeigestil 87 (-139) -64 (-189) = 3}$
   • ${ Anzeigestil 3 = 3}$
   • Da die Gleichheit erfüllt ist, ist die Entscheidung richtig.
6. 6 Schreiben Sie Ausdrücke auf, um viele Lösungen zu finden. Die "x"-Werte entsprechen der ursprünglichen Lösung plus einem beliebigen Vielfachen des "B"-Faktors. Dies kann als folgender Ausdruck geschrieben werden:
   • x (k) = x + k (B), wobei „x (k)“ die Menge der „x“-Werte und „x“ der ursprüngliche (erste) Wert von „x“ ist, den Sie gefunden haben.
     • In unserem Beispiel:
     • ${ Displaystil x (k) = -75-64k}$
   • y (k) = y-k (A), wobei y (k) die Menge der y-Werte und y der ursprüngliche (erste) y-Wert ist, den Sie gefunden haben.
     • In unserem Beispiel:
     • ${ displaystyle y (k) = -102-87k}$