Inhalt

• Schritte

Eine trigonometrische Gleichung enthält eine oder mehrere trigonometrische Funktionen der Variablen "x" (oder einer anderen Variablen). Das Lösen einer trigonometrischen Gleichung bedeutet, einen solchen Wert "x" zu finden, der die Funktion (s) und die Gleichung als Ganzes erfüllt.

• Lösungen für trigonometrische Gleichungen werden in Grad oder Bogenmaß ausgedrückt. Beispiele:

x = /3; x = 5π/6; x = 3π/2; x = 45 Grad; x = 37,12 Grad; x = 178,37 Grad.

• Hinweis: Die Werte der trigonometrischen Funktionen aus Winkeln, ausgedrückt im Bogenmaß, und aus Winkeln, ausgedrückt in Grad, sind gleich. Ein trigonometrischer Kreis mit einem Radius gleich eins dient zur Beschreibung trigonometrischer Funktionen sowie zur Überprüfung der Richtigkeit der Lösung der trigonometrischen Grundgleichungen und Ungleichungen.
• Beispiele für trigonometrische Gleichungen:
  • sinx + sin2x = 1/2; tgx + ctgx = 1,732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cosx = 1.

1. Ein trigonometrischer Kreis mit einem Radius von eins (Einheitskreis).
   • Es ist ein Kreis mit einem Radius gleich eins und Mittelpunkt im Punkt O. Der Einheitskreis beschreibt 4 grundlegende trigonometrische Funktionen der Variablen "x", wobei "x" der Winkel ist, der von der positiven Richtung der X-Achse gegen den Uhrzeigersinn gemessen wird.
   • Wenn "x" ein Winkel auf dem Einheitskreis ist, dann:
   • Die horizontale Achse OAx definiert die Funktion F (x) = cos x.
   • Die vertikale Achse OBy definiert die Funktion F (x) = sin x.
   • Die vertikale Achse AT definiert die Funktion F (x) = tan x.
   • Die horizontale Achse BU definiert die Funktion F (x) = ctg x.

• Der Einheitskreis wird auch verwendet, um grundlegende trigonometrische Gleichungen und Ungleichungen zu lösen (verschiedene Positionen von "x" werden darauf berücksichtigt).

Schritte

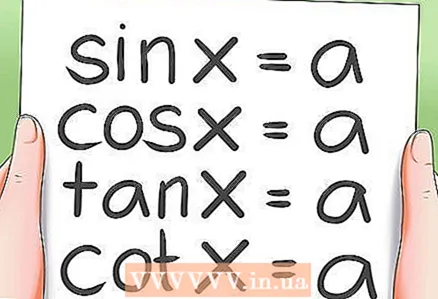1. 1 Das Konzept der Lösung trigonometrischer Gleichungen.
   • Um eine trigonometrische Gleichung zu lösen, konvertieren Sie sie in eine oder mehrere grundlegende trigonometrische Gleichungen. Das Lösen einer trigonometrischen Gleichung läuft letztendlich auf die Lösung von vier grundlegenden trigonometrischen Gleichungen hinaus.
2. 2 Lösen grundlegender trigonometrischer Gleichungen.
   • Es gibt 4 Arten von grundlegenden trigonometrischen Gleichungen:
   • sinx = a; cos x = a
   • tgx = a; ctg x = a
   • Das Lösen grundlegender trigonometrischer Gleichungen beinhaltet das Betrachten der verschiedenen x-Positionen auf dem Einheitskreis und die Verwendung einer Umrechnungstabelle (oder eines Taschenrechners).
   • Beispiel 1.sin x = 0,866. Mit einer Umrechnungstabelle (oder einem Taschenrechner) erhalten Sie die Antwort: x = π / 3. Der Einheitskreis gibt eine andere Antwort: 2π / 3. Denken Sie daran: Alle trigonometrischen Funktionen sind periodisch, dh ihre Werte werden wiederholt. Beispielsweise beträgt die Periodizität von sin x und cos x 2πn und die Periodizität von tg x und ctg x beträgt n. Daher lautet die Antwort wie folgt:
   • x1 = / 3 + 2πn; x2 = 2π / 3 + 2πn.
   • Beispiel 2.cos x = -1/2. Mit einer Umrechnungstabelle (oder einem Taschenrechner) erhalten Sie die Antwort: x = 2π / 3. Der Einheitskreis gibt eine andere Antwort: -2π / 3.
   • x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π.
   • Beispiel 3.tg (x - π / 4) = 0.
   • Antwort: x = π / 4 + πn.
   • Beispiel 4. ctg 2x = 1,732.
   • Antwort: x = π / 12 + πn.
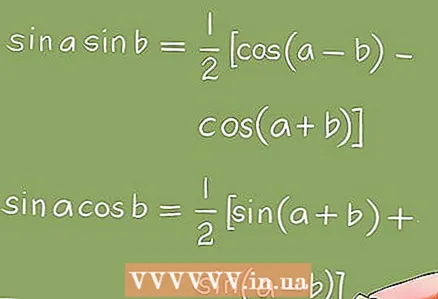3. 3 Transformationen zur Lösung trigonometrischer Gleichungen.
   • Zur Transformation trigonometrischer Gleichungen werden algebraische Transformationen (Faktorisierung, Reduktion homogener Terme usw.) und trigonometrische Identitäten verwendet.
   • Beispiel 5. Unter Verwendung trigonometrischer Identitäten wird die Gleichung sin x + sin 2x + sin 3x = 0 in die Gleichung 4cos x * sin (3x / 2) * cos (x / 2) = 0 transformiert lösen Sie die folgenden trigonometrischen Grundgleichungen: cos x = 0; sin (3x / 2) = 0; cos(x / 2) = 0.
     
     
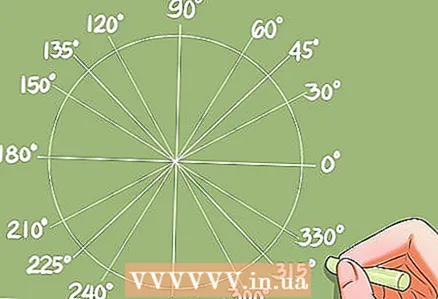4. 4 Finden von Winkeln aus bekannten Werten von Funktionen.
   • Bevor Sie Methoden zum Lösen trigonometrischer Gleichungen erlernen, müssen Sie lernen, Winkel aus bekannten Funktionswerten zu finden. Dies kann mit einer Umrechnungstabelle oder einem Taschenrechner erfolgen.
   • Beispiel: cos x = 0,732. Der Rechner gibt die Antwort x = 42,95 Grad. Der Einheitskreis ergibt zusätzliche Winkel, deren Kosinus ebenfalls 0,732 beträgt.
5. 5 Legen Sie die Lösung auf dem Einheitskreis beiseite.
   • Sie können die Lösungen der trigonometrischen Gleichung auf den Einheitskreis verschieben. Die Lösungen der trigonometrischen Gleichung auf dem Einheitskreis sind die Eckpunkte eines regelmäßigen Vielecks.
   • Beispiel: Die Lösungen x = π / 3 + πn / 2 auf dem Einheitskreis sind die Eckpunkte eines Quadrats.
   • Beispiel: Die Lösungen x = π / 4 + πn / 3 auf dem Einheitskreis repräsentieren die Eckpunkte eines regelmäßigen Sechsecks.
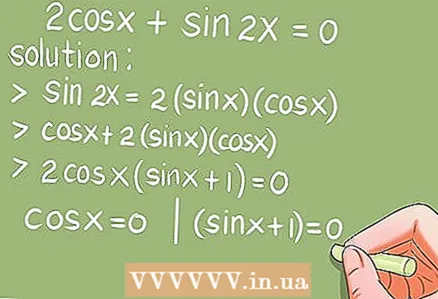6. 6 Methoden zum Lösen trigonometrischer Gleichungen.
   • Wenn eine gegebene trigonometrische Gleichung nur eine trigonometrische Funktion enthält, lösen Sie diese Gleichung als grundlegende trigonometrische Gleichung.Wenn eine gegebene Gleichung zwei oder mehr trigonometrische Funktionen enthält, gibt es 2 Methoden zum Lösen einer solchen Gleichung (abhängig von der Möglichkeit ihrer Transformation).
     • Methode 1.
   • Wandeln Sie diese Gleichung in eine Gleichung der Form um: f (x) * g (x) * h (x) = 0, wobei f (x), g (x), h (x) die grundlegenden trigonometrischen Gleichungen sind.
     
     
   • Beispiel 6.2cos x + sin 2x = 0. (0 x 2π)
   • Lösung. Ersetzen Sie sin 2x mit der Doppelwinkelformel sin 2x = 2 * sin x * cos x.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. Lösen Sie nun die beiden trigonometrischen Grundgleichungen: cos x = 0 und (sin x + 1) = 0.
   • Beispiel 7.cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • Lösung: Transformieren Sie diese Gleichung mit trigonometrischen Identitäten in eine Gleichung der Form: cos 2x (2cos x + 1) = 0. Lösen Sie nun die beiden trigonometrischen Grundgleichungen: cos 2x = 0 und (2cos x + 1) = 0.
   • Beispiel 8.sin x - sin 3x = cos 2x. (0 x 2π)
   • Lösung: Transformieren Sie diese Gleichung mit trigonometrischen Identitäten in eine Gleichung der Form: -cos 2x * (2sin x + 1) = 0. Lösen Sie nun die beiden trigonometrischen Grundgleichungen: cos 2x = 0 und (2sin x + 1) = 0.
     • Methode 2.
   • Wandeln Sie die gegebene trigonometrische Gleichung in eine Gleichung um, die nur eine trigonometrische Funktion enthält. Dann ersetzen Sie diese trigonometrische Funktion durch eine Unbekannte, zum Beispiel t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t usw.).
   • Beispiel 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • Lösung. Ersetze in dieser Gleichung (cos ^ 2 x) durch (1 - sin ^ 2 x) (durch Identität). Die transformierte Gleichung lautet:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. Ersetze sin x durch t. Die Gleichung sieht nun so aus: 5t ^ 2 - 4t - 9 = 0. Dies ist eine quadratische Gleichung mit zwei Wurzeln: t1 = -1 und t2 = 9/5. Die zweite Wurzel t2 erfüllt nicht den Wertebereich der Funktion (-1 sin x 1). Entscheide nun: t = sin x = -1; x = 3π / 2.
   • Beispiel 10.tg x + 2 tg ^ 2 x = ctg x + 2
   • Lösung. Ersetzen Sie tg x durch t. Schreiben Sie die ursprüngliche Gleichung wie folgt um: (2t + 1) (t ^ 2 - 1) = 0. Finden Sie nun t und dann x für t = tg x.
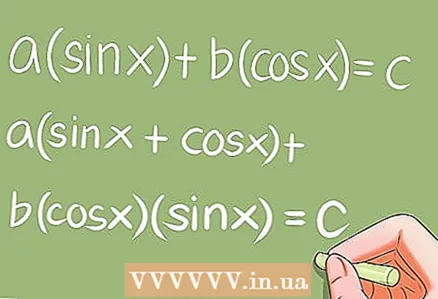7. 7 Spezielle trigonometrische Gleichungen.
   • Es gibt mehrere spezielle trigonometrische Gleichungen, die spezielle Transformationen erfordern. Beispiele:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
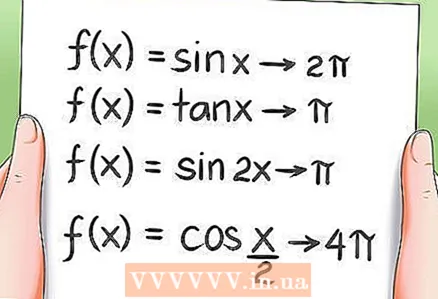8. 8 Periodizität trigonometrischer Funktionen.
   • Wie bereits erwähnt, sind alle trigonometrischen Funktionen periodisch, dh ihre Werte werden nach einer bestimmten Periode wiederholt. Beispiele:
     • Die Periode der Funktion f (x) = sin x beträgt 2π.
     • Die Periode der Funktion f (x) = tan x ist gleich .
     • Die Periode der Funktion f (x) = sin 2x ist π.
     • Die Periode der Funktion f (x) = cos (x / 2) beträgt 4π.
   • Wenn der Zeitraum im Problem angegeben ist, berechnen Sie den Wert "x" innerhalb dieses Zeitraums.
   • Hinweis: Das Lösen trigonometrischer Gleichungen ist keine leichte Aufgabe und führt oft zu Fehlern. Überprüfen Sie Ihre Antworten daher sorgfältig. Um dies zu tun, können Sie einen Grafikrechner verwenden, um die gegebene Gleichung R (x) = 0 zu zeichnen. In solchen Fällen werden Lösungen als Dezimalbrüche dargestellt (dh π wird durch 3,14 ersetzt).