Inhalt

• Schritte
• Methode 1 von 3: Teil 1: Bestimmung des Wendepunktes
• Methode 2 von 3: Berechnung der Ableitungen einer Funktion
• Methode 3 von 3: Teil 3: Finden Sie den Wendepunkt
• Tipps

In der Differentialrechnung ist ein Wendepunkt ein Punkt auf einer Kurve, an dem deren Krümmung das Vorzeichen ändert (von Plus auf Minus oder von Minus auf Plus). Dieses Konzept wird im Maschinenbau, in den Wirtschaftswissenschaften und in der Statistik verwendet, um signifikante Datenänderungen zu erkennen.

Schritte

Methode 1 von 3: Teil 1: Bestimmung des Wendepunktes

1. 1 Definition einer konkaven Funktion. Die Mitte einer beliebigen Sehne (ein Segment, das zwei Punkte verbindet) des Graphen einer konkaven Funktion liegt entweder unter dem Graphen oder auf ihm.
2. 2 Definition einer konvexen Funktion. Die Mitte einer beliebigen Sehne (ein Segment, das zwei Punkte verbindet) des Graphen einer konvexen Funktion liegt entweder über dem Graphen oder auf ihm.
3. 3 Bestimmung der Wurzeln der Funktion. Die Wurzel einer Funktion ist der Wert der Variablen "x", bei dem y = 0 ist.
   • Beim Plotten einer Funktion sind die Wurzeln die Punkte, an denen der Graph die x-Achse schneidet.

Methode 2 von 3: Berechnung der Ableitungen einer Funktion

1. 1 Finden Sie die erste Ableitung der Funktion. Schauen Sie sich die Differenzierungsregeln im Lehrbuch an; Sie müssen lernen, die ersten Ableitungen zu bilden, und erst dann zu komplexeren Berechnungen übergehen. Die ersten Ableitungen werden mit f '(x) bezeichnet. Für Ausdrücke der Form ax ^ p + bx ^ (p − 1) + cx + d lautet die erste Ableitung: apx ^ (p − 1) + b (p - 1) x ^ (p − 2) + c.
   • Finden Sie beispielsweise die Wendepunkte der Funktion f (x) = x ^ 3 + 2x -1. Die erste Ableitung dieser Funktion lautet:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Finden Sie die zweite Ableitung der Funktion. Die zweite Ableitung ist die Ableitung der ersten Ableitung der ursprünglichen Funktion. Die zweite Ableitung wird als f ′ ′ (x) bezeichnet.
   • Im obigen Beispiel lautet die zweite Ableitung:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Setze die zweite Ableitung auf Null und löse die resultierende Gleichung. Das Ergebnis ist der erwartete Wendepunkt.
   • Im obigen Beispiel sieht Ihre Berechnung so aus:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Finden Sie die dritte Ableitung der Funktion. Um zu überprüfen, ob Ihr Ergebnis tatsächlich ein Wendepunkt ist, finden Sie die dritte Ableitung, die die Ableitung der zweiten Ableitung der ursprünglichen Funktion ist. Die dritte Ableitung wird als f ′ ′ ′ (x) bezeichnet.
   • Im obigen Beispiel lautet die dritte Ableitung:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Methode 3 von 3: Teil 3: Finden Sie den Wendepunkt

1. 1 Schau dir die dritte Ableitung an. Die Standardregel zum Schätzen eines Wendepunkts lautet: Wenn die dritte Ableitung nicht null ist (d. h. f ′ ′ ′ (x) 0), dann ist der Wendepunkt der wahre Wendepunkt. Schauen Sie sich die dritte Ableitung an; ist er nicht Null, dann haben Sie den wahren Wendepunkt gefunden.
   • Im obigen Beispiel ist die dritte Ableitung 6, nicht 0.Sie haben also den wahren Wendepunkt gefunden.
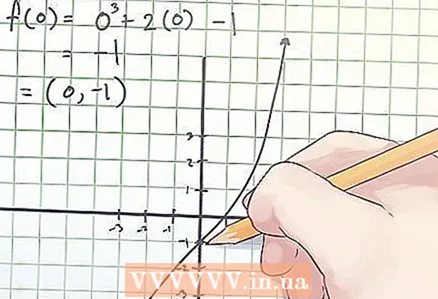2. 2 Finden Sie die Koordinaten des Wendepunkts. Die Wendepunktkoordinaten werden als (x, f (x)) bezeichnet, wobei x der Wert der unabhängigen Variablen „x“ am Wendepunkt ist, f (x) der Wert der abhängigen Variablen „y“ am Wendepunkt ist Punkt.
   • Im obigen Beispiel haben Sie beim Gleichsetzen der zweiten Ableitung mit Null festgestellt, dass x = 0. Um die Koordinaten des Wendepunkts zu bestimmen, finden Sie f (0). Ihre Berechnung sieht so aus:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
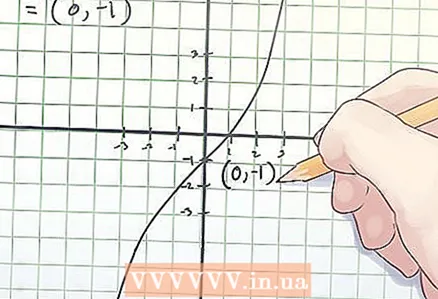3. 3 Notieren Sie die Koordinaten des Wendepunkts. Die Wendepunktkoordinaten sind die gefundenen x- und f(x)-Werte.
   • Im obigen Beispiel liegt der Wendepunkt bei den Koordinaten (0, -1).

Tipps

• Die erste Ableitung eines freien Termes (Primzahl) ist immer Null.