Autor:
Sara Rhodes
Erstelldatum:
14 Februar 2021
Aktualisierungsdatum:
1 Juli 2024
Inhalt
- Schritte
- Methode 1 von 4: Monom im Nenner
- Methode 2 von 4: Binomial im Nenner
- Methode 3 von 4: Umgekehrter Ausdruck
- Methode 4 von 4: Kubischer Wurzelnenner
In der Mathematik ist es nicht üblich, im Nenner eines Bruches eine Wurzel oder eine irrationale Zahl zu belassen. Wenn der Nenner eine Wurzel ist, multiplizieren Sie den Bruch mit einem Term oder Ausdruck, um die Wurzel loszuwerden. Moderne Taschenrechner ermöglichen es Ihnen, mit Wurzeln im Nenner zu arbeiten, aber das Bildungsprogramm erfordert, dass die Schüler in der Lage sind, die Irrationalität im Nenner loszuwerden.
Schritte
Methode 1 von 4: Monom im Nenner
 1 Lerne den Bruch. Der Bruch wird richtig geschrieben, wenn der Nenner keine Wurzel enthält. Wenn der Nenner ein Quadrat oder eine andere Wurzel hat, müssen Sie Zähler und Nenner mit einem Monom multiplizieren, um die Wurzel loszuwerden. Bitte beachten Sie, dass der Zähler eine Wurzel enthalten kann - das ist normal.
1 Lerne den Bruch. Der Bruch wird richtig geschrieben, wenn der Nenner keine Wurzel enthält. Wenn der Nenner ein Quadrat oder eine andere Wurzel hat, müssen Sie Zähler und Nenner mit einem Monom multiplizieren, um die Wurzel loszuwerden. Bitte beachten Sie, dass der Zähler eine Wurzel enthalten kann - das ist normal. - Der Nenner hat hier eine Wurzel
.
 2 Multipliziere Zähler und Nenner mit der Wurzel des Nenners. Wenn der Nenner ein Monom enthält, ist es ziemlich einfach, einen solchen Bruch zu rationalisieren. Multiplizieren Sie Zähler und Nenner mit demselben Monom (dh Sie multiplizieren den Bruch mit 1).
2 Multipliziere Zähler und Nenner mit der Wurzel des Nenners. Wenn der Nenner ein Monom enthält, ist es ziemlich einfach, einen solchen Bruch zu rationalisieren. Multiplizieren Sie Zähler und Nenner mit demselben Monom (dh Sie multiplizieren den Bruch mit 1). - Wenn Sie einen Lösungsausdruck in einen Taschenrechner eingeben, müssen Sie jeden Teil in Klammern setzen, um sie zu trennen.
 3 Vereinfachen Sie den Bruch (wenn möglich). In unserem Beispiel kann es abgekürzt werden, indem Zähler und Nenner durch 7 geteilt werden.
3 Vereinfachen Sie den Bruch (wenn möglich). In unserem Beispiel kann es abgekürzt werden, indem Zähler und Nenner durch 7 geteilt werden.
Methode 2 von 4: Binomial im Nenner
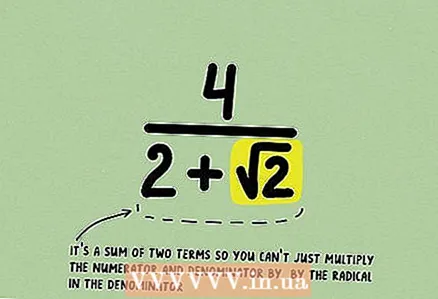 1 Lerne den Bruch. Wenn sein Nenner die Summe oder Differenz zweier Monome enthält, von denen eines eine Wurzel enthält, ist es unmöglich, den Bruch mit einem solchen Binomial zu multiplizieren, um die Irrationalität loszuwerden.
1 Lerne den Bruch. Wenn sein Nenner die Summe oder Differenz zweier Monome enthält, von denen eines eine Wurzel enthält, ist es unmöglich, den Bruch mit einem solchen Binomial zu multiplizieren, um die Irrationalität loszuwerden. - Um dies zu verstehen, schreibe den Bruch auf
wo das monom
oder
enthält die Wurzel. In diesem Fall:
... Somit ist das Monom
wird immer noch die Wurzel enthalten (wenn
oder
enthält die Wurzel).
- Schauen wir uns unser Beispiel an.
- Sie sehen, dass Sie das Monom im Nenner nicht loswerden können
.
 2 Multiplizieren Sie Zähler und Nenner mit dem Binomialkonjugierten des Binoms im Nenner. Ein konjugiertes Binomial ist ein Binomial mit dem gleichen Monom, aber mit dem entgegengesetzten Vorzeichen dazwischen. Zum Beispiel binom
2 Multiplizieren Sie Zähler und Nenner mit dem Binomialkonjugierten des Binoms im Nenner. Ein konjugiertes Binomial ist ein Binomial mit dem gleichen Monom, aber mit dem entgegengesetzten Vorzeichen dazwischen. Zum Beispiel binom zu einem Binomial konjugiert
- Verstehen Sie die Bedeutung dieser Methode. Betrachten Sie den Bruch noch einmal
... Multiplizieren Sie Zähler und Nenner mit dem Binom, das zum Binom im Nenner konjugiert ist:
... Daher gibt es keine Monome, die Wurzeln enthalten. Da die Monome
und
quadriert, werden die Wurzeln eliminiert.
 3 Vereinfachen Sie den Bruch (wenn möglich). Wenn Zähler und Nenner einen gemeinsamen Faktor aufweisen, löschen Sie ihn. In unserem Fall ist 4 - 2 = 2, was verwendet werden kann, um den Bruch zu reduzieren.
3 Vereinfachen Sie den Bruch (wenn möglich). Wenn Zähler und Nenner einen gemeinsamen Faktor aufweisen, löschen Sie ihn. In unserem Fall ist 4 - 2 = 2, was verwendet werden kann, um den Bruch zu reduzieren.
Methode 3 von 4: Umgekehrter Ausdruck
 1 Untersuchen Sie das Problem. Wenn Sie einen Ausdruck finden müssen, der die Umkehrung des gegebenen ist, der eine Wurzel enthält, müssen Sie den resultierenden Bruch rationalisieren (und erst dann vereinfachen). Verwenden Sie in diesem Fall die im ersten oder zweiten Abschnitt beschriebene Methode (je nach Aufgabenstellung).
1 Untersuchen Sie das Problem. Wenn Sie einen Ausdruck finden müssen, der die Umkehrung des gegebenen ist, der eine Wurzel enthält, müssen Sie den resultierenden Bruch rationalisieren (und erst dann vereinfachen). Verwenden Sie in diesem Fall die im ersten oder zweiten Abschnitt beschriebene Methode (je nach Aufgabenstellung). 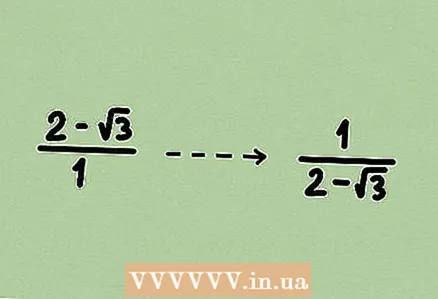 2 Schreiben Sie den gegenteiligen Ausdruck auf. Teilen Sie dazu 1 durch den angegebenen Ausdruck; Wenn ein Bruch gegeben ist, vertausche Zähler und Nenner. Denken Sie daran, dass jeder Ausdruck ein Bruch mit 1 im Nenner ist.
2 Schreiben Sie den gegenteiligen Ausdruck auf. Teilen Sie dazu 1 durch den angegebenen Ausdruck; Wenn ein Bruch gegeben ist, vertausche Zähler und Nenner. Denken Sie daran, dass jeder Ausdruck ein Bruch mit 1 im Nenner ist. 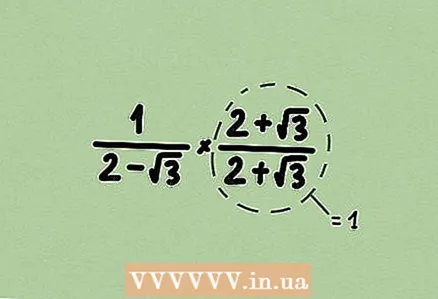 3 Multiplizieren Sie Zähler und Nenner mit einem Ausdruck, um die Wurzel zu entfernen. Indem Sie Zähler und Nenner mit demselben Ausdruck multiplizieren, multiplizieren Sie den Bruch mit 1, dh der Wert des Bruchs ändert sich nicht. In unserem Beispiel erhalten wir ein Binomial, also multiplizieren Sie Zähler und Nenner mit dem konjugierten Binomial.
3 Multiplizieren Sie Zähler und Nenner mit einem Ausdruck, um die Wurzel zu entfernen. Indem Sie Zähler und Nenner mit demselben Ausdruck multiplizieren, multiplizieren Sie den Bruch mit 1, dh der Wert des Bruchs ändert sich nicht. In unserem Beispiel erhalten wir ein Binomial, also multiplizieren Sie Zähler und Nenner mit dem konjugierten Binomial. 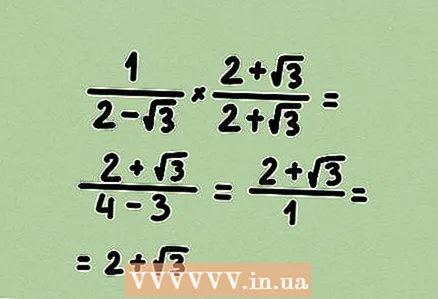 4 Vereinfachen Sie den Bruch (wenn möglich). In unserem Beispiel 4 - 3 = 1, also kann der Ausdruck im Nenner des Bruches komplett gestrichen werden.
4 Vereinfachen Sie den Bruch (wenn möglich). In unserem Beispiel 4 - 3 = 1, also kann der Ausdruck im Nenner des Bruches komplett gestrichen werden. - Die Antwort ist ein zu diesem Binomial konjugiertes Binomial. Es ist nur ein Zufall.
Methode 4 von 4: Kubischer Wurzelnenner
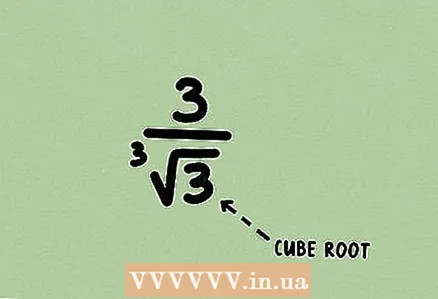 1 Lerne den Bruch. Das Problem kann Kubikwurzeln enthalten, obwohl dies ziemlich selten ist. Das beschriebene Verfahren ist auf Wurzeln jeden Grades anwendbar.
1 Lerne den Bruch. Das Problem kann Kubikwurzeln enthalten, obwohl dies ziemlich selten ist. Das beschriebene Verfahren ist auf Wurzeln jeden Grades anwendbar. 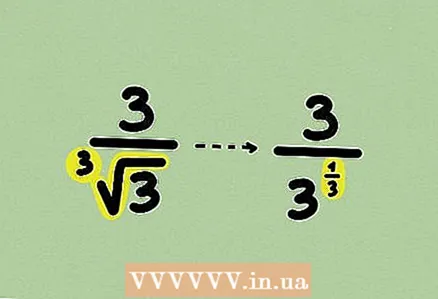 2 Schreiben Sie die Wurzel als Macht um. Hier können Sie Zähler und Nenner nicht mit einem Monom oder Ausdruck multiplizieren, da die Rationalisierung etwas anders erfolgt.
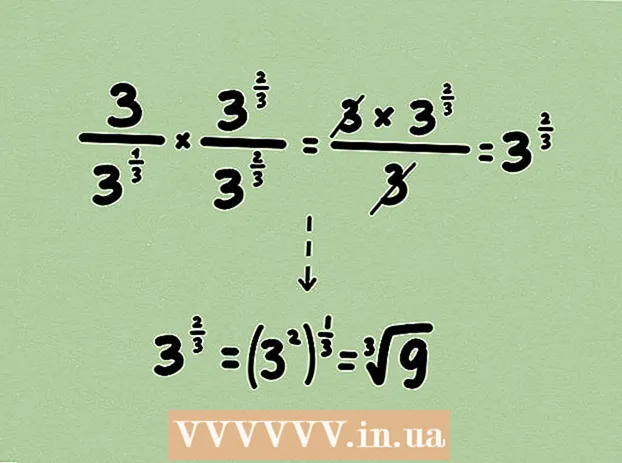
2 Schreiben Sie die Wurzel als Macht um. Hier können Sie Zähler und Nenner nicht mit einem Monom oder Ausdruck multiplizieren, da die Rationalisierung etwas anders erfolgt. 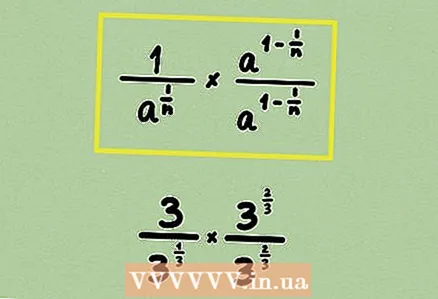 3 Multipliziere Zähler und Nenner des Bruchs mit einer Potenz, sodass der Exponent im Nenner 1 wird. Multiplizieren Sie in unserem Beispiel den Bruch mit
3 Multipliziere Zähler und Nenner des Bruchs mit einer Potenz, sodass der Exponent im Nenner 1 wird. Multiplizieren Sie in unserem Beispiel den Bruch mit ... Denken Sie daran, dass sich ihre Indikatoren addieren, wenn die Grade multipliziert werden:
- Dieses Verfahren ist auf beliebige Wurzeln vom Grad n anwendbar. Wenn ein Bruch gegeben ist
, multipliziere Zähler und Nenner mit
... Somit wird der Exponent im Nenner 1.
 4 Vereinfachen Sie den Bruch (wenn möglich).
4 Vereinfachen Sie den Bruch (wenn möglich).- Notieren Sie bei Bedarf die Wurzel in der Antwort. Zerlegen Sie in unserem Beispiel den Exponenten in zwei Faktoren:
und
.