Inhalt

• Schritte
• Rat

Wenn Sie Mathematiker oder Grafikprogrammierer sind, müssen Sie wahrscheinlich den Winkel zwischen zwei gegebenen Vektoren finden. In diesem Artikel zeigt Ihnen wikiHow, wie Sie genau das tun.

Schritte

Teil 1 von 2: Finden Sie den Winkel zwischen zwei Vektoren

1. 

   Vektordefinition. Notieren Sie alle Informationen zu den beiden Vektoren, die Sie haben. Angenommen, Sie haben nur die angegebenen Parameter ihrer Dimensionskoordinaten (auch Komponenten genannt). Wenn Sie die Länge (Größe) eines Vektors bereits kennen, können Sie einige der folgenden Schritte überspringen.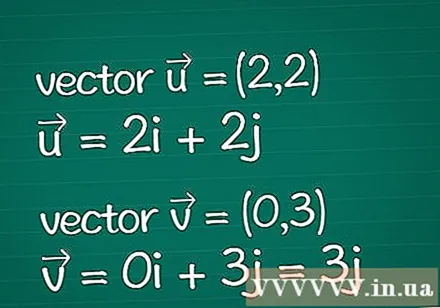
   • Beispiel: Zweidimensionaler Vektor = (2,2) und zweidimensionaler Vektor = (0,3). Sie können auch als = 2 geschrieben werdenich + 2j und = 0ich + 3j = 3j.
   • Obwohl im Beispiel dieses Artikels zweidimensionale Vektoren verwendet werden, können die folgenden Anweisungen für Vektoren mit einer beliebigen Anzahl von Dimensionen gelten.

2. 

   
   
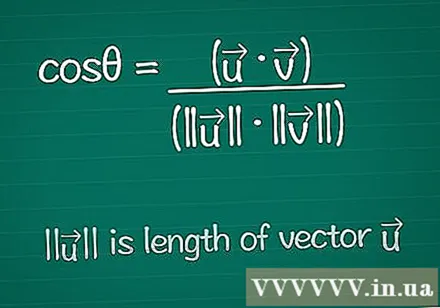
   Schreiben Sie die Kosinusformel auf. Um den Winkel θ zwischen zwei Vektoren zu ermitteln, beginnen wir mit der Formel zum Ermitteln des Kosinus für diesen Winkel. Sie können diese Formel unten kennenlernen oder einfach so aufschreiben:
   • cosθ = (•) / (|||| ||||)
   • |||| bedeutet "Länge des Vektors".
   • • ist das Skalarprodukt der beiden Vektoren - dies wird nachfolgend erläutert.

3. 

   
   
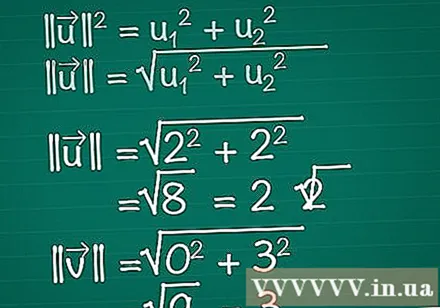
   Berechnen Sie die Länge jedes Vektors. Stellen Sie sich vor, ein rechtwinkliges Dreieck besteht aus den x-, y-Komponenten des Vektors und dem Vektor selbst. Der Vektor bildet die Hypotenuse des Dreiecks. Um seine Länge zu ermitteln, verwenden wir den Satz von Pythagoras. Tatsächlich kann diese Formel leicht auf einen Vektor mit einer beliebigen Anzahl von Dimensionen erweitert werden.
   • || u || = u₁ + u₂. Wenn ein Vektor mehr als zwei Elemente enthält, müssen Sie nur + u hinzufügen₃ + u₄ +...
   • Für einen zweidimensionalen Vektor gilt daher || u || = √ (u₁ + u₂).
   • In diesem Beispiel |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
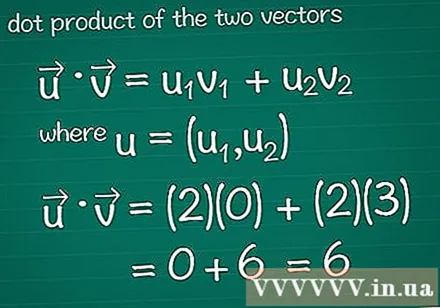
   Berechnen Sie das Skalarprodukt zweier Vektoren. Vielleicht haben Sie die Methode der Vektormultiplikation gelernt, auch bekannt als Skalar Dies. Um das mit ihrer Zusammensetzung verbundene Skalarprodukt zu berechnen, multiplizieren Sie die Inhaltsstoffe in jede Richtung und addieren Sie dann das gesamte Ergebnis.
   • Informationen zum Grafikprogramm finden Sie in den Tipps, bevor Sie weiterlesen.
   • In Mathe • = u₁v₁ + u₂v₂, wo, u = (u₁u₂). Wenn der Vektor mehr als zwei Elemente enthält, fügen Sie einfach + u hinzu₃v₃ + u₄v₄...
   • In diesem Beispiel ist • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dies ist das Skalarprodukt des Vektors und des Vektors.

5. 

   Tragen Sie die Ergebnisse in die Formel ein. Denken Sie daran, dass cosθ = (•) / (|||| || ||). Jetzt kennen wir sowohl das Skalarprodukt als auch die Länge jedes Vektors. Geben Sie diese in die Formel ein, um den Kosinus des Winkels zu berechnen.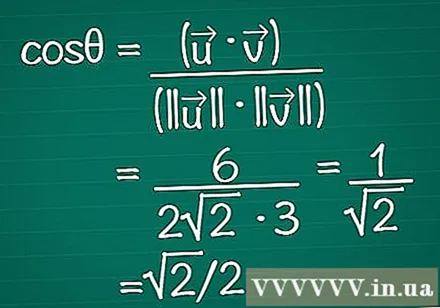
   • In unserem Beispiel ist cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Finden Sie den Winkel basierend auf seinem Kosinus. Sie können die Funktion arccos oder cos in einem Taschenrechner verwenden, um θ aus einem bekannten cos-Wert zu ermitteln. Bei einigen Ergebnissen können Sie den Winkel basierend auf dem Einheitskreis finden.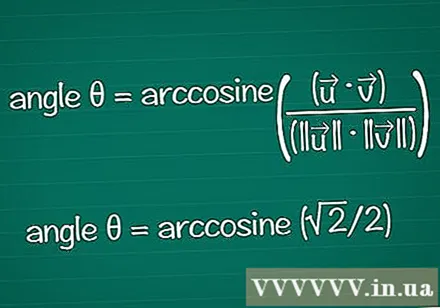
   • Im Beispiel ist cosθ = √2 / 2. Geben Sie "arccos (√2 ​​/ 2)" in Ihren Rechner ein, um den Winkel zu ermitteln. Oder Sie finden den Winkel θ auf dem Einheitskreis an der Position cosθ = √2 / 2. Dies gilt für θ = /₄ oder 45º.
   • Die endgültige Formel lautet: Winkel θ = Arccosin ((•) / (|||| || ||))
   Werbung

Teil 2 von 2: Bestimmung der Winkelformel

1. 

   Verstehe den Zweck der Formel. Diese Formel wurde nicht aus bestehenden Regeln abgeleitet. Stattdessen wird es als Definition des Skalarprodukts und des Winkels zwischen den beiden Vektoren gebildet. Trotzdem war es keine willkürliche Entscheidung. Wenn wir zur Grundgeometrie zurückkehren, können wir verstehen, warum diese Formel intuitive und nützliche Definitionen bietet.
   • In den folgenden Beispielen werden zweidimensionale Vektoren verwendet, da sie am einfachsten zu verstehen und am einfachsten sind. Dreidimensionale oder mehr Vektoren haben Eigenschaften, die durch fast ähnliche allgemeine Formeln definiert sind.

2. 

   Überprüfen Sie den Satz von Cosine. Betrachten Sie ein gewöhnliches Dreieck mit einem Winkel θ zwischen den Seiten a und b gegenüber der Seite c. Der Kosinussatz besagt, dass c = a + b -2ab istcos(θ). Dieses Ergebnis wird ganz einfach aus der Grundgeometrie gezogen.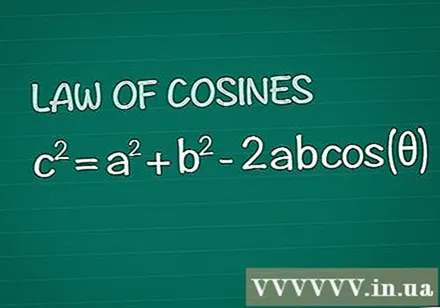

3. 

   Verbinden Sie zwei Vektoren zu einem Dreieck. Zeichnen Sie ein Paar zweidimensionaler Vektoren auf Papier, Vektoren und Vektoren, wobei θ der Winkel zwischen ihnen ist. Zeichnen Sie einen dritten Vektor zwischen diesen beiden, um ein Dreieck zu erstellen. Mit anderen Worten, zeichnen Sie einen Vektor so, dass + =. Vektor = -.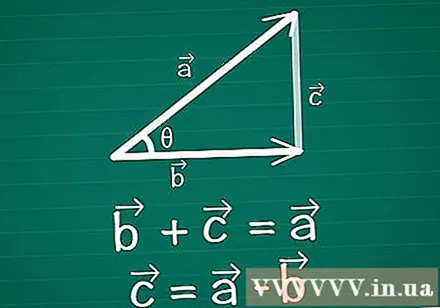

4. 

   Schreiben Sie den Kosinussatz für dieses Dreieck. Setzen Sie die Seitenlänge unseres "Vektordreiecks" in den Kosinussatz ein:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Mit skalarem Produkt umschreiben. Denken Sie daran, ein Skalarprodukt ist das Bild eines Vektors auf dem anderen. Das Skalarprodukt eines Vektors mit sich selbst erfordert keine Projektion, da hier kein Richtungsunterschied besteht. Das heißt • = || a ||. Damit schreiben wir die Gleichung neu:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Die gleiche Formel wurde erfolgreich umgeschrieben. Erweitern Sie die linke Seite der Formel und vereinfachen Sie sie, um die Formel zum Ermitteln von Winkeln zu erhalten.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   Werbung

Rat

• Verwenden Sie diese Formel für jedes Paar zweidimensionaler Vektoren, um Werte zu ändern und das Problem schnell zu lösen: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Wenn Sie mit Computergrafiksoftware arbeiten, müssen Sie sich wahrscheinlich nur um die Vektordimension kümmern, ohne sich um deren Länge kümmern zu müssen. Führen Sie die folgenden Schritte aus, um eine Gleichung zu verkürzen und Ihr Programm zu beschleunigen:
  • Normalisieren Sie jeden Vektor so, dass er 1 ist. Teilen Sie dazu jede der Vektorkomponenten durch ihre Länge.
  • Holen Sie sich das normalisierte Produkt des Skalars anstelle des ursprünglichen Vektors.
  • Da die Länge 1 ist, können wir die Längenelemente aus der Gleichung ausschließen. Schließlich lautet die erhaltene Winkelgleichung arccos (•).
• Anhand der Kosinusformel können wir schnell feststellen, ob der Winkel spitz oder stumpf ist. Beginnen Sie mit cosθ = (•) / (|||| ||||):
  • Die linke und rechte Seite der Gleichung müssen das gleiche Vorzeichen haben (positiv oder negativ).
  • Da die Länge immer positiv ist, muss cosθ das gleiche Vorzeichen wie das Skalarprodukt haben.
  • Wenn das Produkt positiv ist, ist daher auch cosθ positiv. Wir befinden uns im ersten Quadranten des Einheitskreises mit θ <π / 2 oder 90º. Der zu findende Winkel ist der scharfe Winkel.
  • Wenn das Skalarprodukt negativ ist, ist cosθ negativ. Wir befinden uns im zweiten Quadranten des Einheitskreises mit π / 2 <θ ≤ π oder 90º <θ ≤ 180º. Das ist die Gefängnisecke.