Inhalt

• Schritte
• Methode 1 von 4: Radius
• Methode 2 von 4: Nach Durchmesser
• Methode 3 von 4: Umfang
• Methode 4 von 4: Nach Fläche eines Kreissektors

Einige Schüler verstehen nicht, wie man die Fläche eines Kreises aus den Originaldaten ermittelt. Zuerst müssen Sie sich die Formel merken, nach der die Fläche des Kreises berechnet wird: ${ displaystyle S = pi r ^ {2}}$... Die Formel ist einfach: Um die Fläche eines Kreises zu finden, müssen Sie nur seinen Radius kennen. Sie müssen jedoch in der Lage sein, andere Anfangswerte zu transformieren, um diese Formel verwenden zu können.

Schritte

Methode 1 von 4: Radius

1. 1 Finden Sie den Radius des Kreises. Ein Radius ist ein Liniensegment, das den Mittelpunkt des Kreises mit einem beliebigen Punkt am Außenumfang des Kreises verbindet. Der Radius kann in jede Richtung gemessen werden: er wird gleich sein. Der Radius ist auch der halbe Durchmesser des Kreises. Der Durchmesser ist das Liniensegment, das durch den Mittelpunkt des Kreises geht und zwei Punkte am Außenumfang des Kreises verbindet.
   • In der Regel wird der Wert des Radius in den Bedingungen des Problems angegeben. Es ist ziemlich schwierig, den genauen Mittelpunkt eines Kreises zu finden, es sei denn, er ist auf einem auf Papier gezeichneten Kreis markiert.
   • Der Radius eines Kreises beträgt beispielsweise 6 cm.
2. 2 Quadrieren Sie den Radius. Formel zur Berechnung der Fläche eines Kreises: ${ displaystyle S = pi r ^ {2}}$, wo ${ Anzeigestil r}$ - der Radius, der in die zweite Potenz (quadratisch) erhöht wird.
   • Sie müssen nicht die ganze Formel quadrieren.
   • In unserem Beispiel: ${ Anzeigestil r = 6}$, so ${ displaystyle r ^ {2} = 36}$.
3. 3 Multiplizieren Sie das Ergebnis mit pi. Diese Nummer wird mit einem griechischen Buchstaben bezeichnet ${ displaystyle pi}$ und ist eine mathematische Konstante, die die Beziehung zwischen Radius und Fläche eines Kreises charakterisiert. Pi ist ungefähr 3,14. Die genaue Bedeutung von pi umfasst eine unendliche Anzahl von Ziffern. Manchmal wird die Antwort (Bereich des Kreises) mit einer Konstante geschrieben ${ displaystyle pi}$.
   • In unserem Beispiel (r = 6 cm) berechnet sich die Fläche wie folgt:
     • ${ displaystyle S = pi r ^ {2}}$
     • ${ displaystyle S = pi 6 ^ {2}}$
     • ${ displaystyle S = 36 pi}$ oder ${ Anzeigestil S = 36 (3.14) = 113.04}$
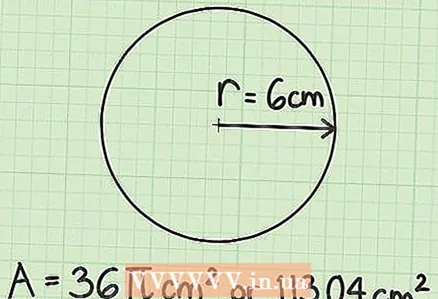4. 4 Schreiben Sie Ihre Antwort auf. Denken Sie daran, dass die Fläche in Quadrateinheiten gemessen wird. Wird der Radius in Zentimetern angegeben, wird die Fläche in Quadratzentimetern gemessen. Wird der Radius in Millimetern angegeben, wird die Fläche in Quadratmillimetern gemessen. Fragen Sie Ihren Lehrer, wenn Sie eine Antwort mit einer Konstante geben müssen ${ displaystyle pi}$ oder numerisch unter Verwendung des ungefähren Wertes von pi. Wenn die Anforderung nicht klar ist, schreiben Sie beide Antworten auf.
   • In unserem Beispiel (r = 6 cm) S = 36${ displaystyle pi}$ cm oder S = 113,04 cm.

Methode 2 von 4: Nach Durchmesser

1. 1 Messen oder notieren Sie den Durchmesser. Bei einigen Problemen wird der Radius nicht angegeben. Anstelle des Radius wird der Durchmesser angezeigt. Wenn der Durchmesser auf Papier gezeichnet ist, messen Sie ihn mit einem Lineal. Höchstwahrscheinlich wird ein numerischer Wert für den Durchmesser angegeben.
   • Der Durchmesser eines Kreises beträgt beispielsweise 20 mm.
2. 2 Den Durchmesser halbieren. Denken Sie daran, dass der Durchmesser das Doppelte des Radius ist. Teilen Sie also jeden Durchmesserwert durch 2, um den Radius zu finden.
   • Wenn der Durchmesser des Kreises also 20 mm beträgt, beträgt der Radius des Kreises 20/2 = 10 mm.
3. 3 Verwenden Sie die Standardformel, um die Fläche eines Kreises zu berechnen. Nachdem Sie den Radius gefunden haben, verwenden Sie die Formel ${ displaystyle S = pi r ^ {2}}$um die Fläche des Kreises zu berechnen. Setzen Sie den Radiuswert ein und berechnen Sie wie folgt:
   • ${ displaystyle S = pi r ^ {2}}$
   • ${ displaystyle S = pi 10 ^ {2}}$
   • ${ displaystyle S = 100 pi}$
4. 4 Schreiben Sie Ihre Antwort auf. Denken Sie daran, dass die Fläche in Quadrateinheiten gemessen wird. In unserem Beispiel wird der Durchmesser in Millimetern angegeben, also auch der Radius in Millimetern und die Fläche in Quadratmillimetern. In unserem Beispiel ist S = ${ displaystyle 100 pi}$ mm.
   • Die Antwort kann auch in numerischer Form dargestellt werden, indem anstelle von . verwendet wird ${ displaystyle pi}$ ein ungefährer Wert von 3,14. In diesem Fall ist S = (100) (3.14) = 314 mm.

Methode 3 von 4: Umfang

1. 1 Schreiben Sie die umgerechnete Formel auf. Wenn Sie den Umfang eines Kreises kennen, können Sie seine Fläche mit der transformierten Formel berechnen. Diese Formel beinhaltet den Umfang, nicht den Radius und wird wie folgt geschrieben: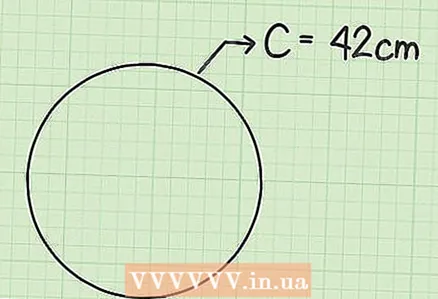
   • ${ displaystyle S = { frac {C ^ {2}} {4 pi}}}$
2. 2 Messen oder notieren Sie den Umfang. In einigen Situationen kann der Durchmesser oder Radius nicht genau gemessen werden. Wenn der Durchmesser nicht gezeichnet oder der Mittelpunkt nicht markiert ist, ist es sehr schwierig, den genauen Mittelpunkt des Kreises zu finden. Der Umfang einiger Gegenstände (z. B. Bratpfannen) lässt sich mit einem Maßband relativ einfach messen, d. h. Sie können einen genaueren Wert für den Umfang als den Durchmesser ermitteln.
   • Der Umfang eines Kreises (oder runden Gegenstands) beträgt beispielsweise 42 cm.
3. 3 Verwenden Sie das Verhältnis zwischen Umfang und Radius, um die Formel neu zu schreiben. Der Umfang ist gleich Pi mal dem Durchmesser. Es kann so geschrieben werden: ${ displaystyle C = pi d}$... Denken Sie daran, dass der Durchmesser gleich dem doppelten Radius ist, also ${ Anzeigestil d = 2r}$... Kombinieren Sie diese Gleichungen, um die folgende Formel zu schreiben: ${ displaystyle C = pi 2r}$... Isolieren Sie nun die Variable ${ Anzeigestil r}$:
   • ${ displaystyle C = pi 2r}$
   • ${ displaystyle { frac {C} {2 pi}} = r}$ (beide Seiten durch 2 teilen${ displaystyle pi}$)
4. 4 Schreiben Sie eine Formel zur Berechnung der Fläche eines Kreises auf. Notieren Sie die umgerechnete Formel basierend auf der Beziehung zwischen dem Umfang und dem Radius. Setzen Sie die letzte Gleichung in die Standardformel zur Berechnung der Fläche eines Kreises ein:
   • ${ displaystyle S = pi r ^ {2}}$ (Standardformel)
   • ${ displaystyle S = pi ({ frac {C} {2 pi}}) ^ {2}}$ (R wurde durch einen Ausdruck ersetzt)
   • ${ displaystyle S = pi ({ frac {C ^ {2}} {4 pi ^ {2}}})}$ (Quadratbruch)
   • ${ displaystyle S = { frac {C ^ {2}} {4 pi}}}$ (reduziert ${ displaystyle pi}$ im Zähler und im Nenner)
5. 5 Verwenden Sie die transformierte Formel, um das Problem zu lösen. In der Formel gibt es jetzt anstelle des Radius einen Umfang, sodass Sie die Fläche eines Kreises mit einem bekannten Umfang berechnen können. Setzen Sie den Umfang ein und berechnen Sie wie folgt:
   • In unserem Beispiel ${ Anzeigestil C = 42}$ cm.
   • ${ displaystyle S = { frac {C ^ {2}} {4 pi}}}$
   • ${ displaystyle S = { frac {42 ^ {2}} {4 pi}}}$ (ersetzter Wert)
   • ${ displaystyle S = { frac {1764} {4 pi}}}$ (berechnet 42)
   • ${ displaystyle S = { frac {441} { pi}}}$ (geteilt durch 4)
6. 6 Schreiben Sie Ihre Antwort auf. Ist der Umfang als Zahl angegeben, nicht als Produkt aus Zahl und ${ displaystyle pi}$, die Antwort kann mit geschrieben werden ${ displaystyle pi}$ im Nenner. Oder ersetzen Sie den ungefähren Wert von Pi (3.14) anstelle von Pi.
   • In unserem Beispiel (C = 42 cm) S = ${ displaystyle { frac {441} { pi}}}$ cm.
   • Oder so: S = ${ displaystyle { frac {441} { pi}} = { frac {441} {3.14}} = 140,4}$ cm.

Methode 4 von 4: Nach Fläche eines Kreissektors

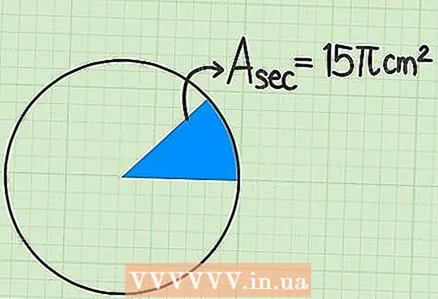1. 1 Notieren Sie die bekannten Werte. Bei einigen Problemen ist die Fläche eines Kreissektors angegeben, anhand derer Sie die Fläche des gesamten Kreises ermitteln müssen. Lesen Sie dieses Problem sorgfältig durch; seine Bedingung kann so aussehen: „Die Fläche des Kreissektors beträgt 15${ displaystyle pi}$ siehe Finde die Fläche des ganzen Kreises. "
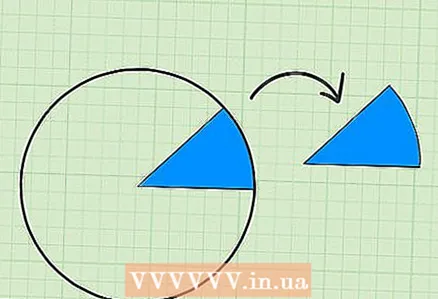2. 2 Denken Sie an die Sektordefinition. Ein Kreissektor ist der Teil eines Kreises, der von einem Bogen und zwei Radien begrenzt wird. Der Raum zwischen solchen Radien und dem Bogen wird als Sektor bezeichnet.
3. 3 Messen Sie den Mittelpunktswinkel des Sektors. Verwenden Sie einen Winkelmesser, um den Winkel zwischen den beiden Radien zu messen. Richten Sie das Lineal (gerade Skala) an einem der Radien aus, und der Mittelpunkt des Lineals sollte mit dem Mittelpunkt des Kreises übereinstimmen. Finden Sie dann den Wert des Winkels; Schauen Sie sich dazu den Schnittpunkt des zweiten Radius mit der goniometrischen Skala an.
   • Verwechseln Sie nicht die Innen- und Außenecke zwischen den beiden Radien. Die Aufgabe sollte angeben, mit welchem ​​Winkel gearbeitet werden soll. Denken Sie daran, dass die Summe der Innen- und Außenwinkel 360 Grad beträgt.
   • Bei vielen Problemen ist der Zentriwinkel angegeben, dh Sie müssen ihn nicht messen. Das Problem kann beispielsweise lauten: "Der Zentralwinkel des Sektors beträgt 45 Grad"; Wenn nicht, messen Sie den Mittelwinkel.
4. 4 Verwenden Sie die umgerechnete Formel, um die Fläche eines Kreises zu berechnen. Wenn Sie die Fläche des Sektors und seinen Mittelpunktswinkel kennen, verwenden Sie die folgende transformierte Formel, um die Fläche eines Kreises zu ermitteln:
   • ${ displaystyle S_ {kr} = S_ {sek} { frac {360} {C}}}$
     • ${ Displaystil S_ {kr}}$ - Fläche eines Kreises
     • ${ displaystyle S_ {sek}}$ - Sektorbereich
     • ${ Anzeigestil C}$ - zentrale Ecke
5. 5 Setze die bekannten Werte ein und finde die Fläche des Kreises. In unserem Beispiel wissen wir, dass der Zentriwinkel 45 Grad beträgt und die Fläche des Sektors 15 . beträgt${ displaystyle pi}$... Setze diese Werte in die Formel ein:
   • ${ displaystyle S_ {kr} = S_ {sek} { frac {360} {C}}}$
   • ${ displaystyle S_ {kr} = 15 pi { frac {360} {45}}}$
   • ${ displaystyle S_ {kr} = 15 pi (8)}$
   • ${ displaystyle S_ {kr} = 120 pi}$
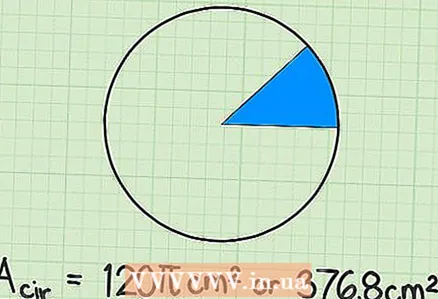6. 6 Schreiben Sie Ihre Antwort auf. In unserem Beispiel war der Sektor ein Achtel eines vollen Kreises. Daher beträgt die Fläche eines Vollkreises 120${ displaystyle pi}$ cm Da die Fläche des Sektors mit einer Konstanten angegeben ist ${ displaystyle pi}$höchstwahrscheinlich kann die Antwort auch mit dieser Konstante dargestellt werden.
   • Um deine Antwort numerisch zu schreiben, multipliziere 120 x 3,14 = 376,8 cm.