Autor:
Robert Simon
Erstelldatum:
21 Juni 2021
Aktualisierungsdatum:
1 Juli 2024
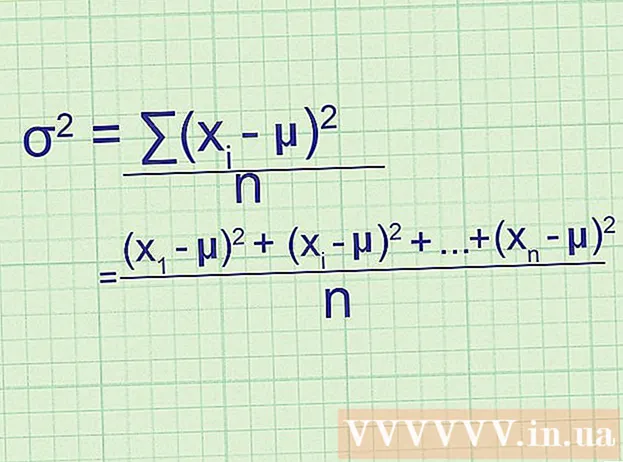
Inhalt
Die Varianz misst die Streuung des Datensatzes. Dies ist beim Erstellen statistischer Modelle sehr nützlich: Eine geringe Varianz kann ein Hinweis darauf sein, dass Sie zufällige Fehler oder Rauschen anstelle der zugrunde liegenden Beziehung in den Daten beschreiben. In diesem Artikel erfahren Sie in wikiHow, wie Sie die Varianz berechnen.
Schritte
Methode 1 von 2: Berechnen Sie die Varianz einer Stichprobe
Schreiben Sie Ihren Beispieldatensatz. In den meisten Fällen verfügen Statistiker nur über Informationen zu einer Stichprobe oder einer Teilmenge der untersuchten Population. Anstatt beispielsweise die "Kosten jedes Autos in Deutschland" zu analysieren, könnte ein Statistiker die Kosten einer Zufallsstichprobe von einigen tausend Autos ermitteln. Der Statistiker kann anhand dieser Stichprobe eine gute Schätzung der Autokosten in Deutschland erhalten. Es ist jedoch wahrscheinlicher, dass es nicht genau mit den tatsächlichen Zahlen übereinstimmt.
- Beispielsweise: Bei der Analyse der Anzahl der pro Tag in einem Café verkauften Muffins haben Sie eine zufällige Sechs-Tage-Stichprobe genommen und die folgenden Ergebnisse erhalten: 38, 37, 36, 28, 18, 14, 12, 11, 10,7, 9,9. Dies ist eine Stichprobe, keine Grundgesamtheit, da Sie nicht für jeden Tag, an dem das Geschäft geöffnet ist, Daten haben.
- Wenn jeden Datenpunkte im Master, bitte gehen Sie zur folgenden Methode.

Notieren Sie die Stichprobenvarianzformel. Die Varianz eines Datensatzes gibt den Grad der Streuung der Datenpunkte an. Je näher die Varianz an Null liegt, desto näher sind die Datenpunkte gruppiert. Verwenden Sie beim Arbeiten mit Beispieldatensätzen die folgende Formel, um die Varianz zu berechnen:- = /(n - 1)
- ist die Varianz. Die Varianz wird immer in quadratischen Einheiten berechnet.
- repräsentiert einen Wert in Ihrem Datensatz.
- ∑, was "Summe" bedeutet, fordert Sie auf, die folgenden Parameter für jeden Wert zu berechnen und sie dann zu addieren.
- x̅ ist der Mittelwert der Stichprobe.
- n ist die Anzahl der Datenpunkte.

Berechnen Sie den Mittelwert der Probe. Das Symbol x̅ oder "x-horizontal" wird verwendet, um den Mittelwert der Probe anzuzeigen. Berechnen Sie wie bei jedem Durchschnitt: Addieren Sie alle Datenpunkte und dividieren Sie sie durch die Anzahl der Punkte.- Beispielsweise: Addieren Sie zunächst Ihre Datenpunkte: 17 + 15 + 23 + 7 + 9 + 13 = 84
Teilen Sie als nächstes das Ergebnis durch die Anzahl der Datenpunkte, in diesem Fall sechs: 84 ÷ 6 = 14.
Stichprobenmittelwert = x̅ = 14. - Sie können sich den Mittelwert als "Mittelpunkt" der Daten vorstellen. Wenn die Daten um den Mittelwert zentriert sind, ist die Varianz gering. Wenn sie weit vom Mittelwert entfernt sind, ist die Varianz hoch.
- Beispielsweise: Addieren Sie zunächst Ihre Datenpunkte: 17 + 15 + 23 + 7 + 9 + 13 = 84

Subtrahieren Sie den Mittelwert von jedem Datenpunkt. Jetzt ist die Zeit zu berechnen - x̅, wo sich jeder Punkt in Ihrem Datensatz befindet. Jedes Ergebnis zeigt eine Abweichung vom Mittelwert jedes entsprechenden Punktes oder einfach ausgedrückt den Abstand von diesem zum Mittelwert an.- Beispielsweise:
- x̅ = 17 - 14 = 3
- x̅ = 15 - 14 = 1
- x̅ = 23 - 14 = 9
- x̅ = 7 - 14 = -7
- x̅ = 9 - 14 = -5
- x̅ = 13 - 14 = -1 - Es ist sehr einfach, Ihre Berechnungen zu überprüfen, da die Ergebnisse zu Null summiert werden müssen. Dies liegt daran, dass durch den Mittelwert der Mittelwert die negativen Ergebnisse (der Abstand vom Mittelwert zu kleinen Zahlen). positive Ergebnisse (Abstand vom Mittelwert zu größeren Zahlen) werden vollständig eliminiert.
- Beispielsweise:
Quadrieren Sie alle Ergebnisse. Wie oben erwähnt, hat die aktuelle Abweichungsliste (- x̅) eine Summe von Null. Das bedeutet, dass die "durchschnittliche Abweichung" auch immer Null ist und nichts über die Streuung der Daten gesagt werden kann. Um dieses Problem zu lösen, finden wir das Quadrat jeder Abweichung. Dank dessen sind alle positive Zahlen, negative Werte und positive Werte, die sich nicht mehr gegenseitig aufheben und die Summe Null ergeben.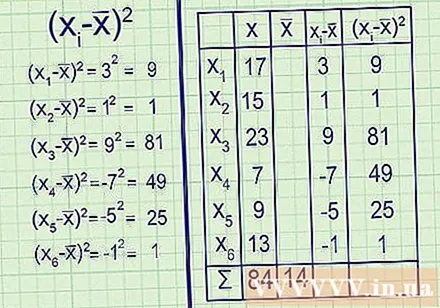
- Beispielsweise:
(- x̅)
- x̅)
9 = 81
(-7) = 49
(-5) = 25
(-1) = 1 - Sie haben jetzt (- x̅) für jeden Datenpunkt in der Stichprobe.
- Beispielsweise:
Finden Sie die Summe der quadratischen Werte. Jetzt ist es an der Zeit, den gesamten Zähler der Formel zu berechnen: ∑. Für den großen Cyclo ∑ müssen Sie für jeden Wert den folgenden Elementwert hinzufügen. Sie haben für jeden Wert in der Stichprobe (- x̅) berechnet. Sie müssen also nur die Ergebnisse addieren.
- Beispielsweise: 9 + 1 + 81 + 49 + 25 + 1 = 166.
Teilen Sie durch n - 1, wobei n die Anzahl der Datenpunkte ist. Vor langer Zeit haben Statistiker bei der Berechnung der Stichprobenvarianz nur durch n geteilt. Diese Division gibt Ihnen den Mittelwert der quadratischen Abweichung, der genau der Varianz dieser Stichprobe entspricht. Beachten Sie jedoch, dass die Stichprobe nur eine Schätzung einer größeren Population darstellt. Wenn Sie eine andere Zufallsstichprobe nehmen und dieselbe Berechnung durchführen, erhalten Sie ein anderes Ergebnis. Wie sich herausstellt, erhalten Sie durch Teilen durch n-1 anstelle von n eine bessere Schätzung der Varianz einer größeren Population - was Ihnen wirklich wichtig ist. Diese Korrektur ist so häufig, dass sie jetzt die akzeptierte Definition der Stichprobenvarianz ist.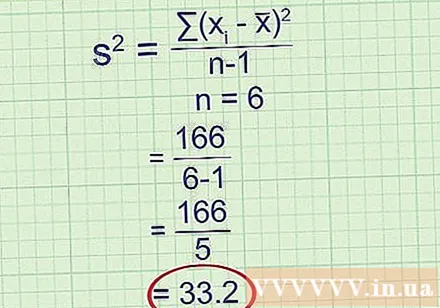
- Beispielsweise: Die Stichprobe enthält sechs Datenpunkte, also n = 6.
Stichprobenvarianz = 33,2
- Beispielsweise: Die Stichprobe enthält sechs Datenpunkte, also n = 6.
Varianz und Standardabweichung verstehen. Beachten Sie, dass die Varianz im Quadrat der Einheiten der Originaldaten gemessen wird, da die Formel Potenzen enthält. Das ist optisch verwirrend. Stattdessen ist häufig die Standardabweichung sehr nützlich. Es macht jedoch keinen Sinn, Mühe zu verschwenden, da die Standardabweichung durch die Quadratwurzel der Varianz bestimmt wird. Aus diesem Grund wird die Stichprobenvarianz als und die Standardabweichung einer Stichprobe als geschrieben.
- Zum Beispiel ist die Standardabweichung der obigen Stichprobe = s = √33,2 = 5,76.
Methode 2 von 2: Berechnen Sie die Varianz einer Population
Beginnend mit dem Stammdatensatz. Der Begriff "Bevölkerung" bezieht sich auf alle relevanten Beobachtungen. Wenn Sie beispielsweise das Alter der Einwohner von Hanoi untersuchen, umfasst Ihre Gesamtbevölkerung das Alter aller in Hanoi lebenden Personen. Normalerweise würden Sie eine Tabelle für einen großen Datensatz wie diesen erstellen, aber hier ist ein kleinerer Beispieldatensatz:
- Beispielsweise: Im Raum eines Aquariums befinden sich genau sechs Aquarien. Diese sechs Tanks enthalten die folgende Anzahl von Fischen:
- Beispielsweise: Im Raum eines Aquariums befinden sich genau sechs Aquarien. Diese sechs Tanks enthalten die folgende Anzahl von Fischen:
Notieren Sie die Formel für die Gesamtvarianz. Da eine Population alle Daten enthält, die wir benötigen, gibt uns diese Formel die genaue Varianz der Population. Um es von der Stichprobenvarianz (die nur eine Schätzung ist) zu unterscheiden, verwenden Statistiker andere Variablen:
- σ = /n
- σ = Stichprobenvarianz. Dies ist die normalerweise quadratische Wurst. Die Varianz wird in quadratischen Einheiten gemessen.
- repräsentiert ein Element in Ihrem Datensatz.
- Das Element in ∑ wird für jeden Wert berechnet und dann addiert.
- μ ist der Gesamtmittelwert.
- n ist die Anzahl der Datenpunkte in der Population.
Finden Sie den Mittelwert der Bevölkerung. Bei der Analyse einer Population repräsentiert das Symbol μ ("mu") das arithmetische Mittel. Um den Mittelwert zu ermitteln, addieren Sie alle Datenpunkte und dividieren Sie sie durch die Anzahl der Punkte.
- Sie können sich Mittelwert als "Durchschnitt" vorstellen, aber seien Sie vorsichtig, da das Wort viele mathematische Definitionen hat.
- Beispielsweise: Mittelwert = μ = = 10,5
Subtrahieren Sie den Mittelwert von jedem Datenpunkt. Datenpunkte, die näher am Mittelwert liegen, weisen eine Differenz auf, die näher an Null liegt. Wiederholen Sie das Subtraktionsproblem für alle Datenpunkte, und Sie werden wahrscheinlich die Streuung der Daten spüren.
- Beispielsweise:
- μ = 5 – 10,5 = -5,5
- μ = 5 – 10,5 = -5,5
- μ = 8 – 10,5 = -2,5
- μ = 12 - 10., = 1,5
- μ = 15 – 10,5 = 4,5
- μ = 18 – 10,5 = 7,5
- Beispielsweise:
Quadrieren Sie jedes Zeichen. Zu diesem Zeitpunkt sind einige Ergebnisse aus dem vorherigen Schritt negativ und einige positiv.Wenn Sie die Daten auf einer isomorphen Linie visualisieren, repräsentieren diese beiden Elemente die Zahlen links und rechts vom Mittelwert. Dies wäre für die Berechnung der Varianz nicht von Nutzen, da sich diese beiden Gruppen gegenseitig aufheben würden. Quadrieren Sie sie stattdessen alle so, dass sie alle positiv sind.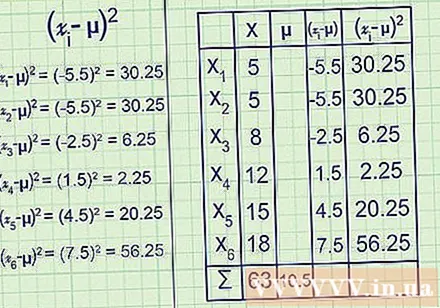
- Beispielsweise:
(- μ) für jeden Wert von ich läuft von 1 bis 6:
(-5,5) = 30,25
(-5,5) = 30,25
(-2,5) = 6,25
(1,5) = 2,25
(4,5) = 20,25
(7,5) = 56,25
- Beispielsweise:
Finden Sie den Durchschnitt Ihrer Ergebnisse. Sie haben jetzt einen Wert für jeden Datenpunkt, der (nicht direkt) damit zusammenhängt, wie weit dieser Datenpunkt vom Mittelwert entfernt ist. Durchschnitt, indem Sie sie addieren und durch die Anzahl Ihrer Werte dividieren.
- Beispielsweise:
Gesamtvarianz = 24,25
- Beispielsweise:
Kontaktrezept. Wenn Sie nicht sicher sind, wie dies zu der zu Beginn der Methode beschriebenen Formel passt, schreiben Sie das gesamte Problem von Hand auf und kürzen Sie nicht ab: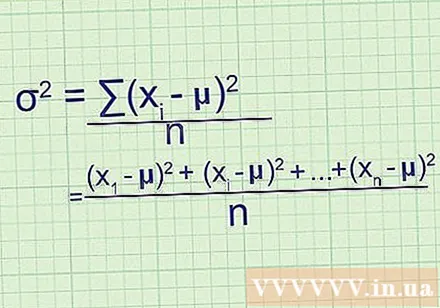
- Nachdem Sie die Differenz zwischen Mittelwert und Quadrat ermittelt haben, erhalten Sie (- μ), (- μ) usw. bis (- μ), wo sich der letzte Datenpunkt befindet. im Datensatz.
- Um den Durchschnitt dieser Werte zu ermitteln, addieren Sie sie und dividieren Sie durch n: ((- μ) + (- μ) + ... + (- μ)) / n
- Nach dem Umschreiben des Zählers mit Sigmoid-Notation haben Sie /n, Formelvarianz.
Rat
- Da die Varianz schwer zu interpretieren ist, wird dieser Wert häufig als Ausgangspunkt für die Ermittlung der Standardabweichung berechnet.
- Die Verwendung von "n-1" anstelle von "n" im Nenner ist eine Technik, die als Bessel-Korrektur bezeichnet wird. Die Stichprobe ist nur eine Schätzung einer vollständigen Population, und der Mittelwert der Stichprobe weist eine gewisse Verzerrung auf, die dieser Schätzung entspricht. Diese Korrektur beseitigt die obige Vorspannung. Es geht um die Tatsache, dass nach der Aufzählung von n - 1 Datenpunkten der letzte Punkt ist n war eine Konstante, da nur bestimmte Werte verwendet wurden, um den Mittelwert der Stichprobe (x̅) in der Varianzformel zu berechnen.



