Inhalt

• Schreiten
• Methode 1 von 3: Eine erste einfache Aufgabe
• Methode 2 von 3: Berechnung des erwarteten Wertes für ein bestimmtes Ergebnis
• Methode 3 von 3: Das Konzept verstehen
• Tipps
• Notwendigkeiten

Der Erwartungswert ist ein statistischer Begriff und ein Konzept, mit dem entschieden wird, wie nützlich oder schädlich eine Aktion sein wird. Um den erwarteten Wert zu berechnen, ist es notwendig, ein gutes Verständnis für jedes Ergebnis in einer bestimmten Situation und die damit verbundene Wahrscheinlichkeit oder die Wahrscheinlichkeit, dass ein bestimmtes Ergebnis auftritt, zu erlangen. Die folgenden Schritte enthalten einige Beispielübungen, die Ihnen helfen, das Konzept des Erwartungswerts zu verstehen.

Schreiten

Methode 1 von 3: Eine erste einfache Aufgabe

1. Lesen Sie die Erklärung. Bevor Sie über alle möglichen Ergebnisse und Wahrscheinlichkeiten nachdenken, ist es wichtig, dass Sie das Problem verstehen. Zum Beispiel ein Würfelspiel, das 10 € pro Spiel kostet. Ein Hex-Würfel wird einmal gewürfelt und Ihr Gewinn hängt von der Anzahl ab, die Sie würfeln. Wenn eine 6 gewürfelt wird, gewinnen Sie 30 €; eine 5 verdient 20 €; jede andere Zahl ergibt nichts.
2. Listen Sie alle möglichen Ergebnisse auf. Es hilft, alle möglichen Ergebnisse in einer bestimmten Situation aufzulisten. Im obigen Beispiel gibt es 6 mögliche Ergebnisse. Dies sind: (1) Wirf eine 1 und du verlierst 10 $, (2) Wirf eine 2 und du verlierst 10 $, (3) Wirf eine 3 und du verlierst 10 $, (4) Wirf eine 4 und du verlierst 10 $ , (5) wirf eine 5 und gewinne 10 $, (6) wirf eine 6 und gewinne 20 $.
   • Beachten Sie, dass jedes Ergebnis 10 € weniger ist als oben beschrieben, da Sie unabhängig vom Ergebnis zuerst 10 € pro Spiel zahlen müssen.
3. Bestimmen Sie die Wahrscheinlichkeit für jedes Ergebnis. In diesem Fall ist die Wahrscheinlichkeit von 6 Ergebnissen gleich. Die Wahrscheinlichkeit, dass eine Zufallszahl gewürfelt wird, beträgt 1 zu 6. Um das Aufschreiben zu vereinfachen, schreiben wir den Bruch (1/6) mit einem Taschenrechner als Dezimalzahl: 0,167. Schreiben Sie diese Wahrscheinlichkeit neben jedes Ergebnis, insbesondere wenn Sie ein Problem mit unterschiedlichen Wahrscheinlichkeiten für jedes Ergebnis lösen möchten.
   • Ihr 1/6 Rechner könnte so etwas wie 0.166667 machen. Wir runden dies auf 0,167, um die Berechnung zu vereinfachen, ohne die Genauigkeit zu beeinträchtigen.
   • Wenn Sie ein sehr genaues Ergebnis wünschen, machen Sie es nicht zu einer Dezimalzahl, geben Sie einfach 1/6 in die Formel ein und berechnen Sie es auf Ihrem Taschenrechner.
4. Notieren Sie den Wert jedes Ergebnisses. Multiplizieren Sie den $ eines Ergebnisses mit der Wahrscheinlichkeit, dass das Ergebnis auftritt, um zu berechnen, wie viel Geld dieses Ergebnis zum erwarteten Wert beiträgt. Zum Beispiel ist das Ergebnis des Würfelns einer 1 - $ 10 und die Wahrscheinlichkeit des Würfelns einer 1 ist 0,167. Der Wert für das Werfen einer 1 ist daher (-10) * (0,167).
   • Diese Ergebnisse müssen jetzt nicht berechnet werden, wenn Sie einen Taschenrechner haben, der mehrere Vorgänge gleichzeitig ausführen kann. Sie erhalten ein genaueres Ergebnis, wenn Sie die gesamte Gleichung eingeben.
5. Addieren Sie den Wert jedes Ergebnisses, um den erwarteten Wert eines Ereignisses zu erhalten. Um mit dem obigen Beispiel fortzufahren, ist der Erwartungswert des Würfelspiels: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167) oder - 1,67 €. Sie können also davon ausgehen, dass Sie bei diesem Spiel jedes Mal (pro Spiel) 1,67 $ verlieren.
6. Welche Auswirkungen hat die Berechnung des erwarteten Werts? Im obigen Beispiel haben wir festgestellt, dass der erwartete Gewinn (Verlust) - 1,67 € pro Wurf betragen würde. Dies ist ein unmögliches Ergebnis für 1 Spiel; Sie können 10 € verlieren, 10 € gewinnen oder 20 € gewinnen. Auf lange Sicht ist der erwartete Wert jedoch eine nützliche Durchschnittswahrscheinlichkeit. Wenn Sie dieses Spiel weiter spielen, verlieren Sie durchschnittlich 1,67 USD pro Spiel. Eine andere Möglichkeit, über den erwarteten Wert nachzudenken, besteht darin, dem Spiel bestimmte Kosten (oder Vorteile) zuzuweisen. Sie sollten dieses Spiel nur spielen, wenn Sie es für wert halten. Genießen Sie es genug, um jedes Mal 1,67 USD dafür auszugeben.
   • Je öfter eine Situation wiederholt wird, desto genauer ist der erwartete Wert eine Darstellung des tatsächlichen Durchschnittsergebnisses. Zum Beispiel spielen Sie das Spiel vielleicht fünfmal hintereinander und verlieren jedes Mal, was zu einem durchschnittlichen Verlust von 10 US-Dollar führt. Wenn Sie das Spiel jedoch 1000 Mal spielen, kommt das durchschnittliche Ergebnis dem erwarteten Wert von - 1,67 € pro Spiel immer näher. Dieses Prinzip wird "das Gesetz der großen Zahlen" genannt.

Methode 2 von 3: Berechnung des erwarteten Wertes für ein bestimmtes Ergebnis

1. Verwenden Sie diese Methode, um die durchschnittliche Anzahl von Münzen zu berechnen, die Sie werfen müssen, bevor ein bestimmtes Muster auftritt. Mit dieser Methode können Sie beispielsweise die erwartete Anzahl der umwerfenden Münzen ermitteln, bis Sie zweimal hintereinander Köpfe haben. Dieses Problem ist etwas kniffliger als ein Standardproblem mit Erwartungswerten. Lesen Sie daher zuerst den obigen Teil dieses Artikels, wenn Sie mit dem Konzept des Erwartungswerts nicht vertraut sind.
2. Angenommen, wir suchen nach einem Wert x. Sie versuchen festzustellen, wie viele Münzen Sie durchschnittlich werfen müssen, um zwei Köpfe hintereinander zu erhalten. Wir machen jetzt einen Vergleich, um die Antwort zu finden. Wir nennen die Antwort, die wir suchen, x. Schritt für Schritt führen wir den notwendigen Vergleich durch. Wir haben derzeit Folgendes:
   • x = ___
3. Überlegen Sie, was passiert, wenn der erste Wurf eine Münze ergibt. Dies wird in der Hälfte der Fälle der Fall sein. In diesem Fall haben Sie einen Rollover "verschwendet", während sich die Chance, einen Kopf zweimal hintereinander zu rollen, nicht geändert hat. Wie beim Münzwurf wird erwartet, dass Sie durchschnittlich oft werfen müssen, bevor Sie zweimal hintereinander einen Kopf bekommen. Mit anderen Worten, Sie würden erwarten, x-mal zu würfeln, plus die, die Sie bereits gespielt haben. In Form einer Gleichung:
   • x = (0,5) (x + 1) + ___
   • Wir werden den leeren Raum ausfüllen, während wir weiter über andere Situationen nachdenken.
   • Sie können Brüche anstelle von Dezimalstellen verwenden, wenn dies einfacher oder notwendiger ist.
4. Denken Sie darüber nach, was passiert, wenn Sie Ihren Kopf werfen. Es besteht eine Wahrscheinlichkeit von 0,5 (oder 1/2), dass Sie beim ersten Mal eine Tasse werfen. Dies scheint dem Ziel näher zu kommen, zweimal hintereinander einen Kopf zu werfen, aber wie viel? Der einfachste Weg, dies herauszufinden, besteht darin, über Ihre Optionen in der zweiten Rolle nachzudenken:
   • Wenn der zweite Wurf eine Münze ist, sind wir wieder am Anfang.
   • Wenn das zweite Mal auch eine Tasse ist, dann sind wir fertig!
5. Erfahren Sie, wie Sie die Wahrscheinlichkeit berechnen, dass zwei Ereignisse auftreten. Wir wissen jetzt, dass Sie eine 50% ige Chance haben, eine Tasse zu werfen, aber wie groß ist die Chance, dass Sie zweimal hintereinander eine Tasse werfen? Um diese Wahrscheinlichkeit zu berechnen, multiplizieren Sie die Wahrscheinlichkeit von beiden. In diesem Fall ist es 0,5 x 0,5 = 0,25. Dies ist natürlich auch die Chance, dass Sie Kopf und Schwanz rollen, da beide eine Chance von 0,5 haben: 0,5 x 0,5 = 0,25.
6. Fügen Sie das Ergebnis für "Köpfe, dann Schwänze" zur Gleichung hinzu. Nachdem wir die Wahrscheinlichkeit berechnet haben, dass dieses Ereignis eintreten wird, können wir mit der Erweiterung der Gleichung fortfahren. Es besteht eine Wahrscheinlichkeit von 0,25 (oder 1/4), dass wir zweimal werfen, ohne vorwärts zu gehen. Aber jetzt brauchen wir durchschnittlich noch x mehr Würfe, um das gewünschte Ergebnis zu erzielen, plus die 2, die wir bereits geworfen haben. In Gleichungsform wird dies zu (0,25) (x + 2), was wir nun zur Gleichung hinzufügen können:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + ___
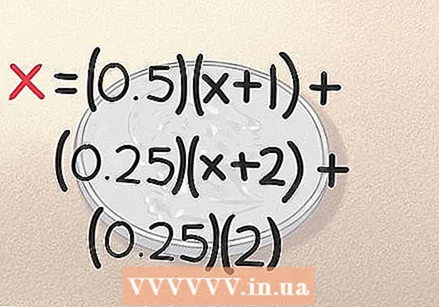7. Fügen Sie das Ergebnis für "Überschrift, Überschrift" zur Gleichung hinzu. Wenn Sie Kopf, Kopf mit den ersten beiden Münzwürfen rollen, sind Sie fertig. Sie haben das Ergebnis in genau 2 Würfen erhalten. Wie bereits erwähnt, besteht eine Wahrscheinlichkeit von 0,25, dass dies geschieht. Die Gleichung hierfür lautet also (0,25) (2). Unser Vergleich ist jetzt abgeschlossen:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + (0,25) (2)
   • Wenn Sie nicht sicher sind, ob Sie alle möglichen Situationen durchdacht haben, können Sie auf einfache Weise überprüfen, ob die Gleichung vollständig ist. Die erste Zahl in jedem Teil der Gleichung gibt die Wahrscheinlichkeit an, mit der ein Ereignis auftritt. Dies ergibt immer 1. Hier ist 0,5 + 0,25 + 0,25 = 1, sodass wir wissen, dass wir jede Situation berücksichtigt haben.
8. Vereinfachen Sie die Gleichung. Lassen Sie uns die Gleichung durch Multiplizieren etwas vereinfachen. Denken Sie daran, wenn Sie in Klammern Folgendes sehen: (0,5) (x + 1), multiplizieren Sie 0,5 mit jedem Term, der in der zweiten Gruppe von Klammern steht. Dies gibt Ihnen Folgendes: 0,5x + (0,5) (1) oder 0,5x + 0,5. Lassen Sie uns dies für jeden Term in der Gleichung tun und dann diese Terme kombinieren, damit alles ein bisschen einfacher aussieht:
   • x = 0,5x + (0,5) (1) + 0,25x + (0,25) (2) + (0,25) (2)
   • x = 0,5x + 0,5 + 0,25x + 0,5 + 0,5
   • x = 0,75x + 1,5
9. Löse nach x. Wie in jeder Gleichung müssen Sie das x auf einer Seite der Gleichung isolieren, um es zu berechnen. Denken Sie daran, x bedeutet "die durchschnittliche Anzahl von Münzen, die Sie werfen müssen, um zweimal hintereinander Köpfe zu bekommen." Wenn wir x berechnet haben, haben wir auch unsere Antwort gefunden.
   • x = 0,75x + 1,5
   • x - 0,75x = 0,75x + 1,5 - 0,75x
   • 0,25x = 1,5
   • (0,25x) / (0,25) = (1,5) / (0,25)
   • x = 6
   • Im Durchschnitt müssen Sie 6 Mal eine Münze werfen, bevor Sie zweimal Köpfe werfen.

Methode 3 von 3: Das Konzept verstehen

1. Was ist eigentlich ein erwarteter Wert? Der Erwartungswert ist nicht unbedingt das offensichtlichste oder logischste Ergebnis. Manchmal kann ein Erwartungswert in einer bestimmten Situation sogar ein unmöglicher Wert sein. Beispielsweise kann der Erwartungswert + 5 € für ein Spiel mit einem Preis von nicht mehr als 10 € betragen. Der Erwartungswert gibt an, wie viel Wert ein bestimmtes Ereignis hat. Wenn ein Spiel einen erwarteten Wert von + 5 € hat, können Sie es spielen, wenn Sie der Meinung sind, dass es die Zeit und das Geld wert ist, die Sie pro Spiel erhalten können. Wenn ein anderes Spiel einen erwarteten Wert von - 20 $ hat, spielen Sie es nur, wenn Sie der Meinung sind, dass jedes Spiel 20 $ wert ist.
2. Verstehen Sie das Konzept unabhängiger Ereignisse. Im Alltag denken viele von uns, dass wir einen glücklichen Tag haben, an dem einige gute Dinge passieren, und wir erwarten, dass der Rest des Tages so verläuft.Ebenso können wir denken, dass wir genug von einem Unfall hatten und dass jetzt wirklich etwas Spaßiges getan werden muss. Mathematisch gesehen laufen die Dinge nicht so. Wenn Sie eine normale Münze werfen, besteht genau die gleiche Chance, dass Sie einen Kopf oder eine Münze werfen. Es spielt keine Rolle, wie oft Sie bereits geworfen haben; Wenn Sie das nächste Mal werfen, funktioniert es immer noch genauso. Der Münzwurf ist "unabhängig" von den anderen Würfen, er ist davon nicht betroffen.
   • Der Glaube, dass Sie Glück oder Pech haben können, wenn Sie Münzen werfen (oder ein anderes Glücksspiel), oder Die Tatsache, dass all Ihr Pech nun beendet ist und das Glück auf Ihrer Seite ist, wird auch als Spielerbetrug (oder als Trugschluss des Spielers) bezeichnet. Dies hat mit der Tendenz der Menschen zu tun, riskante oder dumme Entscheidungen zu treffen, wenn sie das Gefühl haben, dass das Glück auf ihrer Seite ist, oder wenn sie das Gefühl haben, "Glückssträhne" zu haben oder wenn sie das Gefühl haben, dass sich ihr "Glück bald dreht".
3. Verstehe das Gesetz der großen Zahlen. Sie könnten denken, dass der Erwartungswert nicht wirklich nützlich ist, da er Ihnen nur selten sagt, was das tatsächliche Ergebnis einer Situation ist. Wenn Sie berechnet haben, dass der erwartete Wert eines Roulette-Spiels - 1 € beträgt und Sie das Spiel dreimal spielen, erhalten Sie normalerweise - 10 € oder + 60 € oder ein anderes Ergebnis. Das "Gesetz der großen Zahlen" erklärt, warum der Erwartungswert nützlicher ist, als Sie vielleicht denken: Je mehr Sie spielen, desto näher am Erwartungswert liegt das durchschnittliche Ergebnis. Wenn Sie sich die große Anzahl von Ereignissen ansehen, besteht eine gute Chance, dass das Endergebnis nahe am erwarteten Wert liegt.

Tipps

• In Situationen, in denen mehrere Ergebnisse möglich sind, können Sie im Computer eine Tabelle erstellen, um den erwarteten Wert anhand der Ergebnisse und ihrer Wahrscheinlichkeiten zu berechnen.
• Die obigen € -Berechnungen funktionieren auch in anderen Währungen.

Notwendigkeiten

• Bleistift
• Papier
• Taschenrechner